题目内容
已知实数a>0,且2a,1,a2+3按某种顺序排列成等差数列.
(Ⅰ)求实数a的值;
(Ⅱ)若等差数列{an}的首项和公差都为a,等比数列{bn}的首项和公比都为a,数列{an}和{bn}的前n项和分别为Sn,Tn,且
>Sn-238,求满足条件的自然数n的最大值.
(Ⅰ)求实数a的值;
(Ⅱ)若等差数列{an}的首项和公差都为a,等比数列{bn}的首项和公比都为a,数列{an}和{bn}的前n项和分别为Sn,Tn,且
| Tn+2 |
| 2n |
考点:等差数列的性质,等差数列的前n项和
专题:等差数列与等比数列
分析:(Ⅰ)分类讨论,三项分别为等差中项,解方程可得;
(Ⅱ)由(Ⅰ)可得an和bn,进而可得Sn和Tn,代入已知可得n的不等式,解不等式结合n为自然数可得.
(Ⅱ)由(Ⅰ)可得an和bn,进而可得Sn和Tn,代入已知可得n的不等式,解不等式结合n为自然数可得.
解答:
解(Ⅰ)①若2a为等差中项,则有4a=a2+4解得a=2,符合题意;
②若1为等差中项,则有2=2a+a2+3解得a=-1,不符合题意,(舍去);
③若a2+3为等差中项,则有2(a2+3)=2a+1,即2a2-2a+5=0,△<0方程无解;
综上可得a=2
(Ⅱ)由(Ⅰ)知an=2+2(n-1)=2n,bn=2n,
∴Sn=
=n2+n,Tn=
=2n+1-2,
由已知
>Sn-238可得2>n2+n-238,即n(n+1)<240,
即-16<n<15,又n为正整数,n的最大值为14.
②若1为等差中项,则有2=2a+a2+3解得a=-1,不符合题意,(舍去);
③若a2+3为等差中项,则有2(a2+3)=2a+1,即2a2-2a+5=0,△<0方程无解;
综上可得a=2
(Ⅱ)由(Ⅰ)知an=2+2(n-1)=2n,bn=2n,
∴Sn=
| n(2+2n) |
| 2 |
| 2(1-2n) |
| 1-2 |
由已知
| Tn+2 |
| 2n |
即-16<n<15,又n为正整数,n的最大值为14.
点评:本题主要考查等差数列、等比数列等基础知识,考查运算求解能力和应用意识,考查分类整合的思想,属中档题.

练习册系列答案
相关题目
已知复数z满足z(1-i)=2i,其中i为虚数单位,则|z|=( )
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
 已知椭圆C:
已知椭圆C: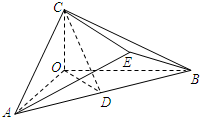 如图,在三棱锥C-OAB中,CO⊥平面AOB,OA=OB=2OC=2,AB=2
如图,在三棱锥C-OAB中,CO⊥平面AOB,OA=OB=2OC=2,AB=2