题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
(Ⅰ)求椭圆C1和抛物线C2的方程;
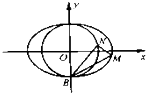
(Ⅱ)如图点B位于椭圆短轴的下端点,M,N分别是椭圆和圆x2+y2=1位于y轴右侧的动点,且直线BN的斜率是直线BN斜率的2倍.证明:直线MN过定点并求出其坐标.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件求出x0=2-
,将A(2-
,2)代入抛物线y2=2px(p>0),求出抛物线方程为y2=4x,从而得到F2(1,0),由此能求出椭圆方程.
(Ⅱ)设直线BM:y=kx-1,直线BN:y=2kx-1,由已知条件推导出MN的方程为y=-
x+1,由此能证明直线MN过定点(0,1).
| p |
| 2 |
| p |
| 2 |
(Ⅱ)设直线BM:y=kx-1,直线BN:y=2kx-1,由已知条件推导出MN的方程为y=-
| 1 |
| 2k |
解答:
(Ⅰ)解:∵点A(x0,2)在抛物线y2=2px(p>0)上,|AF2|=2.
∴|AF2|=x0+
=2,解得x0=2-
,
将A(2-
,2)代入抛物线y2=2px(p>0),
解得p=2,…(2分)
∴抛物线方程为y2=4x…(3分)
∵椭圆C:
+y2=1(a>1)的左右焦点分别为F1,F2,
其中F2也是抛物线C2:y2=2px(p>0)的焦点,
∴F2(1,0),在椭圆中c=1,∴a2=2…(4分)
∴椭圆方程为
+y2=1. …(6分)
(Ⅱ)证明:设BN的斜率为k,则直线BN的斜率为2k,
又两直线均过定点B(0,-1),
设直线BM:y=kx-1,直线BN:y=2kx-1…(7分)
由
,得方程(1+2k2)x2-4kx=0,
xM=
,yM=
…(8分)
同理由
,得方程(1+4k2)x2-4kx=0,
xN=
,yN=
.…(9分)
∴kMN=
=-
…(11分)
∴MN的方程为y-
=-
(x-
),
化简得:y=-
x+1
∴直线MN过定点(0,1)…(13分)
∴|AF2|=x0+
| p |
| 2 |
| p |
| 2 |
将A(2-
| p |
| 2 |
解得p=2,…(2分)
∴抛物线方程为y2=4x…(3分)
∵椭圆C:
| x2 |
| a2 |
其中F2也是抛物线C2:y2=2px(p>0)的焦点,
∴F2(1,0),在椭圆中c=1,∴a2=2…(4分)
∴椭圆方程为
| x2 |
| 2 |
(Ⅱ)证明:设BN的斜率为k,则直线BN的斜率为2k,
又两直线均过定点B(0,-1),
设直线BM:y=kx-1,直线BN:y=2kx-1…(7分)
由
|
xM=
| 4k |
| 2k2+1 |
| 2k2-1 |
| 2k2+1 |
同理由
|
xN=
| 4k |
| 2k2+1 |
| 4k2-1 |
| 2k2+1 |
∴kMN=
| yM-yN |
| xM-xN |
| 1 |
| 2k |
∴MN的方程为y-
| 2k2-1 |
| 2k2+1 |
| 1 |
| 2k |
| 4k |
| 2k2+1 |
化简得:y=-
| 1 |
| 2k |
∴直线MN过定点(0,1)…(13分)
点评:本题考查椭圆的抛物线方程的求法,考查直线过定点的证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
阅读如图所示的程序框图,运行相应的程序.若输入的x∈[0,2),则输出的结果可能是( )


| A、-1 | B、0 | C、1.5 | D、3 |
已知sinα-cosα=
,则cos2(
-α)=( )
| 1 |
| 3 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

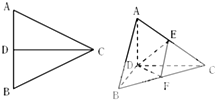 已知正△ABC的边长为a,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
已知正△ABC的边长为a,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.