题目内容
已知抛物线C：y2=8x与点M（-2，2），过C的焦点，且斜率为k的直线与C交于A，B两点，若
•
=0，则k= ．
| MA |
| MB |
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：斜率k存在，设直线AB为y=k（x-2），代入抛物线方程，利用
•
=（x1+2，y1-2）•（x2+2，y2-2）=0，即可求出k的值．
| MA |
| MB |
解答：
解：由抛物线C：y2=8x得焦点（2，0），
由题意可知：斜率k存在，设直线AB为y=k（x-2），
代入抛物线方程，得到k2x2-（4k2+8）x+4k2=0，△＞0，
设A（x1，y1），B（x2，y2）．
∴x1+x2=4+
，x1x2=4．
∴y1+y2=
，y1y2=-16
又
•
=0，
∴
•
=（x1+2，y1-2）•（x2+2，y2-2）=
-
+4=0
∴k=2．
故答案为：2．
由题意可知：斜率k存在，设直线AB为y=k（x-2），
代入抛物线方程，得到k2x2-（4k2+8）x+4k2=0，△＞0，
设A（x1，y1），B（x2，y2）．
∴x1+x2=4+
| 8 |
| k2 |
∴y1+y2=
| 8 |
| k |
又
| MA |
| MB |
∴
| MA |
| MB |
| 16 |
| k2 |
| 16 |
| k |
∴k=2．
故答案为：2．
点评：本题考查直线与抛物线的位置关系，考查向量的数量积公式，考查学生的计算能力，属于中档题．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
某学习小组男女生共8人，现从男生中选2人，女生中选1人，分别去做3中不同的工作，共有90种不同的选法，则男女生人数为（ ）
| A、2，6 | B、3，5 |
| C、5，3 | D、6，2 |
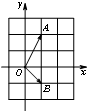如图，在复平面内，若复数z1，z2对应的向量分别是| OA |
| OB |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
集合A={x|x2+x-6＜0}，B={y|y=lg（x2+1）}，则A∩B等于（ ）
| A、（-3，2） |
| B、[0，3） |
| C、[0，+∞） |
| D、[0，2） |