题目内容
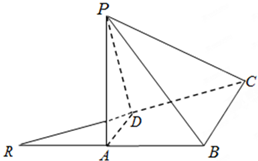 如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.
如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.(1)求证:BC⊥PB;
(2)求二面角A-CD-P的平面角的余弦值.
考点:二面角的平面角及求法,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(1)由已知得点B在以点D为圆心,RC为半径的圆上,∠RBC=90°,∠PAD=∠RAD=∠RBC=90°由此能证明BC⊥PB.
(2)取RD的中点F,连结AF、PF,推导出∠AFP是二面角A-CD-P的平面角,由此能求出二面角A-CD-P的平面角的余弦值.
(2)取RD的中点F,连结AF、PF,推导出∠AFP是二面角A-CD-P的平面角,由此能求出二面角A-CD-P的平面角的余弦值.
解答:
(1)证明:∵点D是RC的中点,且2BD=RC,
所以点B在以点D为圆心,RC为半径的圆上,
所以∠RBC=90°,…(2分)
又因为点A是RB的中点,
∴AD∥BC,AD=
BC,
∴∠PAD=∠RAD=∠RBC=90°,∴PA⊥AD,∴PA⊥BC,
∵BC⊥AB,PA∩AB=A,∴BC⊥平面PAB,…(4分)
∵PB?平面PAB,∴BC⊥PB.…(6分)
(2)解:取RD的中点F,连结AF、PF,
∵RA=AD=1,∴AF⊥RC,
∵AP⊥AR,AP⊥AD,∴AP⊥平面RBC,
∵RC?平面RBC,∴RC⊥AP,
∵AF∩AP=A,
∴RC⊥平面PAF,∵PF?平面PAF,∴RC⊥PF,
∴∠AFP是二面角A-CD-P的平面角,…(9分)
在Rt△RAD中,AF=
RD=
=
,
在Rt△PAF中,PF=
=
,cos∠AFP=
=
=
.
∴二面角A-CD-P的平面角的余弦值是
.…(12分)
所以点B在以点D为圆心,RC为半径的圆上,
所以∠RBC=90°,…(2分)
又因为点A是RB的中点,
∴AD∥BC,AD=
| 1 |
| 2 |
∴∠PAD=∠RAD=∠RBC=90°,∴PA⊥AD,∴PA⊥BC,

∵BC⊥AB,PA∩AB=A,∴BC⊥平面PAB,…(4分)
∵PB?平面PAB,∴BC⊥PB.…(6分)
(2)解:取RD的中点F,连结AF、PF,
∵RA=AD=1,∴AF⊥RC,
∵AP⊥AR,AP⊥AD,∴AP⊥平面RBC,
∵RC?平面RBC,∴RC⊥AP,
∵AF∩AP=A,
∴RC⊥平面PAF,∵PF?平面PAF,∴RC⊥PF,
∴∠AFP是二面角A-CD-P的平面角,…(9分)
在Rt△RAD中,AF=
| 1 |
| 2 |
| 1 |
| 2 |
| RA2+AD2 |
| ||
| 2 |
在Rt△PAF中,PF=
| PA2+AF2 |
| ||
| 2 |
| AF |
| PF |
| ||||
|
| ||
| 3 |
∴二面角A-CD-P的平面角的余弦值是
| ||
| 3 |
点评:本题考查异面直线垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
使得(x+
)n(n∈N*)的展开式中含有常数项的最小的n是( )
| 1 | ||
x
|
| A、4 | B、5 | C、6 | D、7 |
在R上定义运算?:x?y=(1-x)y,若对任意x>2,不等式x?(x-m)≤m+2都成立,则实数m的取值范围是( )
| A、[-1,7] |
| B、(-∞,7] |
| C、(-∞,3] |
| D、(-∞,-1]∪[7,+∞) |
设a、b是两条不同的直线,α、β是两个不同的平面,则下面四个命题中错误的是( )
| A、若a⊥b,a⊥α,b?α,则b∥α |
| B、若a⊥b,a⊥α,b⊥β,则α⊥β |
| C、若a⊥β,α⊥β,则a∥α或a?α |
| D、若 a∥α,α⊥β,则a⊥β |
若正数a,b,c成公差不为零的等差数列,则( )
| A、lga,lgb,lgc成等差数列 |
| B、lga,lgb,lgc成等比数列 |
| C、2a,2b,2c成等差数列 |
| D、2a,2b,2c成等比数列 |
若某多面体的三视图如图所示,则此多面体外接球的表面积是( )


| A、6 | ||||
B、
| ||||
| C、12π | ||||
| D、3π |
 在三棱锥P-ABC中,PA⊥底面ABC,AD⊥平面PBC,其垂足D落在直线PB上,
在三棱锥P-ABC中,PA⊥底面ABC,AD⊥平面PBC,其垂足D落在直线PB上,