题目内容
在R上定义运算?:x?y=(1-x)y,若对任意x>2,不等式x?(x-m)≤m+2都成立,则实数m的取值范围是( )
| A、[-1,7] |
| B、(-∞,7] |
| C、(-∞,3] |
| D、(-∞,-1]∪[7,+∞) |
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:根据新定义,分离参数,原不等式化为m≤
.构造函数,利用基本不等式求出函数的最值,问题得以解决.
| x2-x+2 |
| x-2 |
解答:
解:∵x?y=x(1-y),
∴(x-a)?x≤m+2转化为(x-m)(1-x)≤m+2,
∴-x2+x+mx-m≤m+2,
m(x-2)≤x2-x+2,
∵任意x>2,不等式(x-m)?x≤a+2都成立,
∴m≤
.
令f(x)=
,x>2,
则m≤[f(x)]min,
而f(x)=
=
=(x-2)+
+3≥2
+3=7,当且仅当x=4时,取最小值.
∴m≤7.
故选:B.
∴(x-a)?x≤m+2转化为(x-m)(1-x)≤m+2,
∴-x2+x+mx-m≤m+2,
m(x-2)≤x2-x+2,
∵任意x>2,不等式(x-m)?x≤a+2都成立,
∴m≤
| x2-x+2 |
| x-2 |
令f(x)=
| x2-x+2 |
| x-2 |
则m≤[f(x)]min,
而f(x)=
| x2-x+2 |
| x-2 |
| (x-2)2+3(x-2)+4 |
| x-2 |
| 4 |
| x-2 |
(x-2)•
|
∴m≤7.
故选:B.
点评:本题考查了在新定义下对函数恒成立问题的应用,解答此题的关键是理解定义,并会用定义来解题,属中档题.

练习册系列答案
相关题目
在二项式(2x+1)6的展开式中,系数最大项的系数是( )
| A、20 | B、160 |
| C、240 | D、192 |
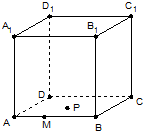 如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且PB,点AM=
如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且PB,点AM=| 1 |
| 3 |
| A、圆 | B、抛物线 | C、双曲线 | D、椭圆 |
下列命题中的真命题是( )
A、?x∈R,sinx+
| ||
B、?x∈R,
| ||
| C、命题p:“?x∈R,x2-x-1>0”的否定¬p:“?x∈R,x2-x-1≤0” | ||
| D、“ea>eb”是“log2a>log2b”的充要条件 |
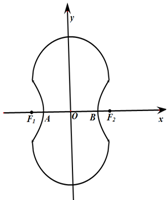 如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2-4y-4=0,双曲线的左、右顶
如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2-4y-4=0,双曲线的左、右顶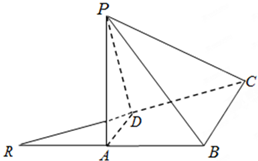 如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.
如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.