题目内容
已知cosφ=-
,180°<φ<270°,求sin2φ,cos2φ,tan2φ的值.
| ||
| 3 |
考点:二倍角的正弦,二倍角的余弦
专题:计算题,三角函数的求值
分析:运用同角的平方关系,求出sinφ,再由二倍角的正弦、余弦和正切公式,即可计算得到.
解答:
解:cosφ=-
,180°<φ<270°,
则sinφ=-
=-
,
即有sin2φ=2sinφcosφ=2×(-
)×(-
)=
;
cos2φ=2cos2φ-1=2×(-
)2-1=-
;
tan2φ=
=
=-2
.
| ||
| 3 |
则sinφ=-
1-(-
|
| ||
| 3 |
即有sin2φ=2sinφcosφ=2×(-
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
cos2φ=2cos2φ-1=2×(-
| ||
| 3 |
| 1 |
| 3 |
tan2φ=
| sin2φ |
| cos2φ |
| ||||
-
|
| 2 |
点评:本题考查同角的平方关系和二倍角的正弦、余弦和正切公式,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
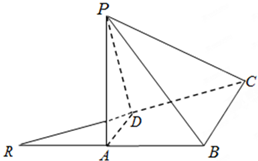 如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.
如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.