题目内容
若某多面体的三视图如图所示,则此多面体外接球的表面积是( )


| A、6 | ||||
B、
| ||||
| C、12π | ||||
| D、3π |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图可知:该几何体是正方体的内接正四面体.可得此多面体外接球的直径是次正方体的对角线
.即可得出.
| 3 |
解答:
解:由三视图可知:该几何体是正方体的内接正四面体(红颜色).
 ∴此多面体外接球的直径是此正方体的对角线
∴此多面体外接球的直径是此正方体的对角线
.
因此其球的表面积是4π(
)2=3π.
故选:D.
 ∴此多面体外接球的直径是此正方体的对角线
∴此多面体外接球的直径是此正方体的对角线| 3 |
因此其球的表面积是4π(
| ||
| 2 |
故选:D.
点评:本题考查了正方体的三视图、球的表面积计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
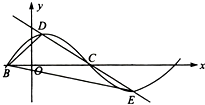 已知函数f(x)=Asin(πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则(
已知函数f(x)=Asin(πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则(| BD |
| BE |
| BE |
| CE |
| A、-1 | ||
B、-
| ||
C、
| ||
| D、2 |
下列命题中的真命题是( )
A、?x∈R,sinx+
| ||
B、?x∈R,
| ||
| C、命题p:“?x∈R,x2-x-1>0”的否定¬p:“?x∈R,x2-x-1≤0” | ||
| D、“ea>eb”是“log2a>log2b”的充要条件 |
阅读下面程序框图,则输出结果s的值为( )


A、
| ||||
B、
| ||||
C、-
| ||||
| D、0 |
若复数z满足zi=1-i(i为虚数单位),则复数z等于( )
| A、1+i | B、-1-i |
| C、1-i | D、-1+i |
设两条直线的方程分别为x+y+a=0,x+y+b=0,已知a,b是方程x2+x+c=0的两个实根,且0≤c≤
,则这两条直线之间的距离的最大值和最小值分别是( )
| 1 |
| 8 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
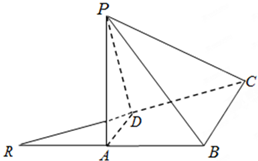 如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.
如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.