题目内容
若正数a,b,c成公差不为零的等差数列,则( )
| A、lga,lgb,lgc成等差数列 |
| B、lga,lgb,lgc成等比数列 |
| C、2a,2b,2c成等差数列 |
| D、2a,2b,2c成等比数列 |
考点:等差关系的确定
专题:等差数列与等比数列
分析:由正数a,b,c成公差不为零的等差数列得到b-a=c-b=d,只要判断2b÷2a=2c÷2b即可.
解答:
解:因为正数a,b,c成公差不为零的等差数列,设公差为d,则b-a=c-b=d,
则2b÷2a=2b-a=2d,2c÷2b=2c-b=2d,
所以2b-a=2c-b,
所以2a,2b,2c成等比数列.
故选D.
则2b÷2a=2b-a=2d,2c÷2b=2c-b=2d,
所以2b-a=2c-b,
所以2a,2b,2c成等比数列.
故选D.
点评:本题考查了等差数列和等比数列的性质;如果三个a,b,c数成等差数列,则2b=a+c;如果三个数啊a,b,c成等比数列,则b2=ac.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
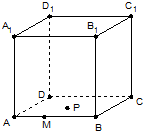 如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且PB,点AM=
如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且PB,点AM=| 1 |
| 3 |
| A、圆 | B、抛物线 | C、双曲线 | D、椭圆 |
阅读下面程序框图,则输出结果s的值为( )


A、
| ||||
B、
| ||||
C、-
| ||||
| D、0 |
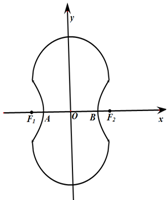 如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2-4y-4=0,双曲线的左、右顶
如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2-4y-4=0,双曲线的左、右顶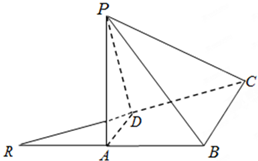 如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.
如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.