题目内容

使得(x+
1
x
x
)n（n∈N*）的展开式中含有常数项的最小的n是（　　）
A、4B、5C、6D、7
考点：二项式系数的性质
专题：二项式定理
分析：在二项展开式的通项公式中，令x的幂指数等于0，求出n和r的关系，即可求得n的最小值．
解答： 解：(x+
1
x
x
)n（n∈N*）的展开式的通项公式为 Tr+1=
C
r
n
•xn-
5r
2
，
令n-
5r
2
=0，可得n=
5r
2
，故当r=2时，n取得最小值为5，
故选：B．
点评：本题主要考查二项式定理的应用，求展开式中某项的系数，二项式系数的性质，属于基础题．
练习册系列答案
相关题目
某班共有60名学生，现领到10张听取学术报告的入场券，先用抽签法和随机数表法把10张入场券分发下去，试写出过程．
已知函数f（x）=|x-a|+|x-1|，a∈R．
（1）当a=3时，解不等式f（x）≤4；
（2）当x∈（-2，1）时，f（x）＞|2x-a-1|，求a的取值范围．
已知函数f（x）=ax+2ln（ax+1），其中实常a∈（1，6）．
（Ⅰ）当a=2时，比较f（x）与6x2+6x的大小；
（Ⅱ）已知函数f（x）的图象与直线y=6x相切，证明x∈（1，3）时，（x+3）f（
x
-1
2
）＜6x-6．
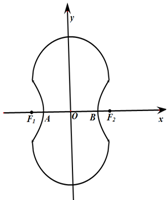如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形，其中上半个圆所在圆方程是x2+y2-4y-4=0，双曲线的左、右顶
点A、B是该圆与x轴的交点，双曲线与半圆相交于与x轴平行的直径的两端点．
（1）试求双曲线的标准方程；
（2）记双曲线的左、右焦点为F1、F2，试在“8”字形曲线上求点P，使得
∠F1PF2是直角．
对于给定数列{cn}，如果存在实常数p，q使得cn+1=pcn+q对于任意n∈N*都成立，我们称数列{cn}是“线性数列”．
（1）若an=2n，bn=3•2n，n∈N*，数列{an}、{bn}是否为“线性数列”？若是，指出它对应的实常数p&，q，若不是，请说明理由；
（2）证明：若数列{an}是“线性数列”，则数列{an+an+1}也是“线性数列”；
（3）若数列{an}满足a1=2，an+an+1=3t•2n（n∈N*），t为常数．求数列{an}前n项的和．
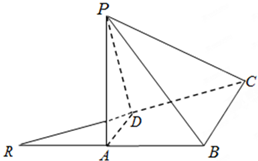如图，△RBC中，RB=BC=2，点A、D分别是RB、RC的中点，且2BD=RC，边AD折起到△PAD位置，使PA⊥AB，连结PB、PC．
（1）求证：BC⊥PB；
（2）求二面角A-CD-P的平面角的余弦值．
解方程x log3xloga3=
x2
a
，x=
 
．
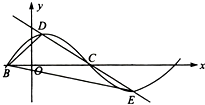已知函数f（x）=Asin（πx+φ）的部分图象如图所示，点B，C是该图象与x轴的交点，过点C的直线与该图象交于D，E两点，则(
BD
+
BE
)•(
BE
-
CE
)的值为（　　）
A、-1
B、-
1
2
C、
1
2
D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网