题目内容
设a、b是两条不同的直线,α、β是两个不同的平面,则下面四个命题中错误的是( )
| A、若a⊥b,a⊥α,b?α,则b∥α |
| B、若a⊥b,a⊥α,b⊥β,则α⊥β |
| C、若a⊥β,α⊥β,则a∥α或a?α |
| D、若 a∥α,α⊥β,则a⊥β |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系求解.
解答:
解:若a⊥b,a⊥α,b?α,则由直线与平面平行的判定定理得b∥α,故A正确;
若a⊥b,a⊥α,b⊥β,则由平面与平面垂直的判定定理得α⊥β,故B正确;
若a⊥β,α⊥β,则线面垂直、面面垂直的性质得a∥α或a?α,故C正确;
若a∥α,α⊥β,则a与β相交、平行或a?β,故D错误.
故选:D.
若a⊥b,a⊥α,b⊥β,则由平面与平面垂直的判定定理得α⊥β,故B正确;
若a⊥β,α⊥β,则线面垂直、面面垂直的性质得a∥α或a?α,故C正确;
若a∥α,α⊥β,则a与β相交、平行或a?β,故D错误.
故选:D.
点评:本题考查命题真假的判断,是基础题,解题时要注意空间思维能力的培养.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
在△ABC中,已知∠BAC=150°,且
•
=-4
,设D是△ABC内部的一点,△DAB、△DBC、△DCA的面积依次为m、n、p,则当p=1时,
+
的最小值为( )
| AB |
| AC |
| 3 |
| 1 |
| m |
| 4 |
| n |
| A、3 | B、5 | C、7 | D、9 |
已知函数f(x)=x2+mx-2n,m,n∈[0,2],则使f(1)≤0成立的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
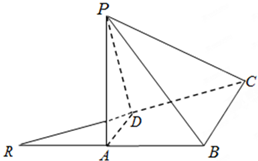 如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.
如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.