题目内容
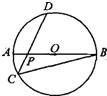
设F1、F2是双曲线
-
=1的两个焦点,若双曲线上存在点M使∠F1MF2=60°,且|MF1|-2|MF2|=0,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
考点:双曲线的简单性质
专题:计算题,解三角形,圆锥曲线的定义、性质与方程
分析:首先判断M在双曲线的右支上,则由双曲线的定义,可得,|MF1|-|MF2|=2a,求得△F1MF2的三边,再由余弦定理,化简整理,运用离心率公式,即可得到所求.
解答:
解:由于|MF1|-2|MF2|=0,
则M在双曲线的右支上,
则由双曲线的定义,可得,|MF1|-|MF2|=2a,
解得|MF1|=4a,|MF2|=2a,
在△F1MF2中,由余弦定理,可得,
cos60°=
即为
=
,
化简可得,c=
a,
则离心率e=
=
.
故选A.
则M在双曲线的右支上,
则由双曲线的定义,可得,|MF1|-|MF2|=2a,
解得|MF1|=4a,|MF2|=2a,
在△F1MF2中,由余弦定理,可得,
cos60°=
| |MF1|2+|MF2|2-|F1F2|2 |
| 2|MF1|•|MF2| |
即为
| 1 |
| 2 |
| 16a2+4a2-4c2 |
| 2×4a•2a |
化简可得,c=
| 3 |
则离心率e=
| c |
| a |
| 3 |
故选A.
点评:本题考查双曲线的定义、方程和性质,考查离心率的求法,考查余弦定理的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=x2+mx-2n,m,n∈[0,2],则使f(1)≤0成立的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
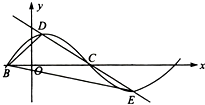 已知函数f(x)=Asin(πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则(
已知函数f(x)=Asin(πx+φ)的部分图象如图所示,点B,C是该图象与x轴的交点,过点C的直线与该图象交于D,E两点,则(| BD |
| BE |
| BE |
| CE |
| A、-1 | ||
B、-
| ||
C、
| ||
| D、2 |
若复数z满足zi=1-i(i为虚数单位),则复数z等于( )
| A、1+i | B、-1-i |
| C、1-i | D、-1+i |
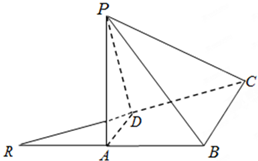 如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.
如图,△RBC中,RB=BC=2,点A、D分别是RB、RC的中点,且2BD=RC,边AD折起到△PAD位置,使PA⊥AB,连结PB、PC.