题目内容
已知矩形ABCD的顶点都在半径为R的球O的球面上，AB=6，BC=2
，棱锥O-ABCD的体积为8
，则球O的表面积为（ ）
| 3 |
| 3 |
| A、16π | B、32 |
| C、48π | D、64π |
考点：球的体积和表面积
专题：空间位置关系与距离
分析：由题意求出矩形的对角线的长，即截面圆的直径，根据棱锥的体积计算出球心距，进而求出球的半径，代入球的表面积公式，可得答案．
解答：
解：由题可知矩形ABCD所在截面圆的半径即为ABCD的对角线长度的一半，
∵AB=6，BC=2
，
∴r=
=2
，
由矩形ABCD的面积S=AB•BC=12
，
则O到平面ABCD的距离为h满足：
×12
h=8
，
解得h=2，
故球的半径R=
=4，
故球的表面积为：4πR2=64π，
故选：D
∵AB=6，BC=2
| 3 |
∴r=
| ||||
| 2 |
| 3 |
由矩形ABCD的面积S=AB•BC=12
| 3 |
则O到平面ABCD的距离为h满足：
| 1 |
| 3 |
| 3 |
| 3 |
解得h=2，
故球的半径R=
| r2+h2 |
故球的表面积为：4πR2=64π，
故选：D
点评：本题是基础题，考查球内几何体的体积的计算，考查计算能力，空间想象能力，常考题型．
练习册系列答案
相关题目
已知点P是直线3x+4y+5=0上的动点，点Q为圆（x-2）2+（y-2）2=4上的动点，则|PQ|的最小值为（ ）
A、
| ||
| B、2 | ||
C、
| ||
D、
|
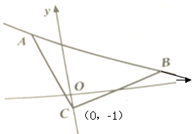如图，等腰直角△ABC的直角顶点C（0，-1），斜边AB所在的直线方程为x+2y-8=0．