题目内容
已知函数f(x)=
,若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是( )
|
| A、[2,3] |
| B、(2,3) |
| C、[2,3) |
| D、(2,3] |
考点:函数的图象
专题:函数的性质及应用
分析:利用分段函数的定义作出函数f(x)的图象,然后可令f(a)=f(b)=f(c)=k则可得a,b,c即为函数y=f(x)与y=k的交点的横坐标根据图象可得出a,b,c的范围同时a,b还满足-log2a=log2b,即可得答案.
解答:
 解:根据已知画出函数图象:
解:根据已知画出函数图象:
不妨设a<b<c,
∵f(a)=f(b)=f(c),
∴-log2a=log2b=-c2+4c-3,
∴log2(ab)=0,
解得ab=1,2<c<3,
∴2<abc<3.
故选:B
 解:根据已知画出函数图象:
解:根据已知画出函数图象:不妨设a<b<c,
∵f(a)=f(b)=f(c),
∴-log2a=log2b=-c2+4c-3,
∴log2(ab)=0,
解得ab=1,2<c<3,
∴2<abc<3.
故选:B
点评:本题考查了利用分段函数的图象结合数形结合的思想求方程根的积得取值范围,由题意正确画出图象和熟练掌握对数函数的图象是解题的关键.

练习册系列答案
相关题目
在正方体ABCD-A′B′C′D′中,点P在线段AD′上运动,则异面直线CP与BA′所成的角θ的取值范围是( )
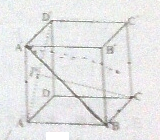

A、0<θ<
| ||
B、0<θ≤
| ||
C、0≤θ≤
| ||
D、0<θ≤
|
已知x,y是两个具有线性相关关系的变量,现有这两个变量的十个样本点(x1,y1)(x2,y2),…,(x10,y10),同学甲利用最小二乘法得到回归直线l1:y=bx+a,同学乙将十个样本点中的两个点连起来得到拟合直线l2:y=dx+c,则下列判断一定正确的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|

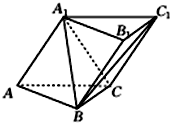 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC.
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC.