题目内容
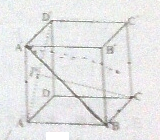
在正方体ABCD-A′B′C′D′中,点P在线段AD′上运动,则异面直线CP与BA′所成的角θ的取值范围是( )

A、0<θ<
| ||
B、0<θ≤
| ||
C、0≤θ≤
| ||
D、0<θ≤
|
考点:异面直线及其所成的角
专题:空间角
分析:由A1B∥D1C,得CP与A1B成角可化为CP与D1C成角,由此能求出异面直线CP与BA′所成的角θ的取值范围.
解答:
解:∵A1B∥D1C,
∴CP与A1B成角可化为CP与D1C成角.
∵△AD1C是正三角形可知当P与A重合时成角为
,
∵P不能与D1重合因为此时D1C与A1B平行而不是异面直线,
∴0<θ≤
.
故选:D.

∴CP与A1B成角可化为CP与D1C成角.
∵△AD1C是正三角形可知当P与A重合时成角为
| π |
| 3 |
∵P不能与D1重合因为此时D1C与A1B平行而不是异面直线,
∴0<θ≤
| π |
| 3 |
故选:D.
点评:本题考查直线与平面所成角的取值范围的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
一个正三棱柱恰好有一个内切球(球与三棱柱的两个底面和三个侧面都相切)和一个外接球(球经过三棱柱的6个顶点),则此内切球与外接球表面积之比为( )
| A、1:3 | B、1:5 |
| C、1:7 | D、1:9 |
已知正四棱柱ABCD-A1B1C1D1中,AB=2,CC1=2
,E为CC1的中点,则直线BE与AC1所成角的余弦值为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
执行程序框图,输出的结果为( )


| A、9 | B、8 | C、6 | D、4 |
已知函数f(x)=
,若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是( )
|
| A、[2,3] |
| B、(2,3) |
| C、[2,3) |
| D、(2,3] |
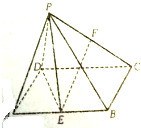 如图,在四棱锥P-ABCD中,底面为矩形ABCD,E,F分别为AB,PC的中点,且PD=PE,PB=PC,求证:
如图,在四棱锥P-ABCD中,底面为矩形ABCD,E,F分别为AB,PC的中点,且PD=PE,PB=PC,求证: