题目内容
已知极坐标系的极点在平面直角坐标系的原点O处,极轴与x轴的非负半轴重合,且长度单位相同,若圆C的极坐标方程为ρ=2cosθ,直线l的参数方程为
(t为参数),直线l与圆C交于A,B两点.
(1)求圆C的直角坐标方程与直线l的普通方程;
(2)求AB的长.
|
(1)求圆C的直角坐标方程与直线l的普通方程;
(2)求AB的长.
考点:参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:(1)将直线l的参数方程的参数t消去即可求出直线的普通方程,利用极坐标转化成直角坐标的转换公式求出圆的直角坐标方程;
(2)线l过圆心C(2,2),即可求AB的长.
(2)线l过圆心C(2,2),即可求AB的长.
解答:
解:(1)由ρ=2cosθ,得ρ2=2ρcosθ,
所以圆C的直角坐标方程为x2+y2=2x,即(x-1)2+y2=1.…(5分)
直线l的普通方程为2x-y-2=0.…(10分)
(2)因为直线l过圆心C(2,2),所以AB=2.…(14分)
所以圆C的直角坐标方程为x2+y2=2x,即(x-1)2+y2=1.…(5分)
直线l的普通方程为2x-y-2=0.…(10分)
(2)因为直线l过圆心C(2,2),所以AB=2.…(14分)
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,把参数方程化为普通方程的方法,比较基础.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
下列命题中的假命题是( )
| A、以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的旋转体叫圆柱 |
| B、以直角三角形的一条边所在的直线为旋转轴,其余两边旋转形成的曲面的旋转体叫圆锥 |
| C、以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面围成的旋转体叫圆锥 |
| D、以等腰三角形的底边上的高所在直线为旋转轴,其余各边旋转形成的曲面围成的旋转体叫圆锥 |
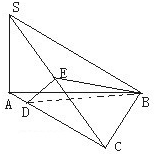 已知SA⊥平面ABC,SA=AB,AB⊥BC,SB=BC,E是SC的中点,DE⊥SC交AC于D.
已知SA⊥平面ABC,SA=AB,AB⊥BC,SB=BC,E是SC的中点,DE⊥SC交AC于D.