Question

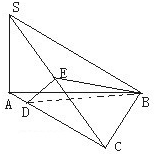已知SA⊥平面ABC，SA=AB，AB⊥BC，SB=BC，E是SC的中点，DE⊥SC交AC于D．
（1）求证：SC⊥面BDE；
（2）求二面角E-BD-C的大小．

Answer 1

考点：二面角的平面角及求法,直线与平面垂直的判定

专题：空间位置关系与距离,空间角

分析：（1）由等腰三角形的性质得BE⊥SC，再由DE⊥SC，能证明SC⊥面BDE．
（2）先证明二面角的棱BD垂直于平面SAC，从而得出了二面角的平面角为∠EDC，故求二面角的大小转化成了求∠EDC的大小．

解答： （1）证明：∵SB=BC，E是SC的中点，
∴BE⊥SC，
∵DE⊥SC交AC于D，BE∩DE=E，
∴SC⊥面BDE．
（2）解：∵SC⊥面BDE，∴SC⊥BD，
∵SA⊥平面ABC，BD?平面ABC，∴SA⊥BD，
∵SA∩SC=S，∴BD⊥平面SAC，
∴∠EDC是二面角E-BD-C的平面角，设SA=a，则SB=BC=

2

a，
∵BC⊥AB，SA⊥平面ABC，
∴BC⊥SB．∴SC=2a，∠SCD=30°．
∴∠EDC=60°，
即二面角EBDC的大小是60°．

点评：本题考查直线与平面垂直的证明，考查二面角的求法，是中档题，解题时要认真审题，注意空间思维能力的合理运用．