题目内容
下列命题中,错误的是( )
| A、在△ABC中,A>B是sinA>sinB的充要条件 |
| B、在锐角△ABC中,不等式sinA>cosB恒成立 |
| C、在△ABC中,若acosA=bcosB,则△ABC必是等腰直角三角形 |
| D、在△ABC中,若B=60°,b2=ac,则△ABC必是等边三角形 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.在△ABC中,由正弦定理可得
=
,可得sinA>sinB?a>b?A>B,即可判断出正误;
B.在锐角△ABC中,由
>A>
-B>0,可得sinA>sin(
-B)=cosB,即可判断出正误;
C.在△ABC中,由acosA=bcosB,利用正弦定理可得:sin2A=sin2B,得到2A=2B或2A=2π-2B即可判断出正误;
D.在△ABC中,利用余弦定理可得:b2=a2+c2-2accosB,代入已知可得a=c,又B=60°,即可得到△ABC的形状,即可判断出正误.
| a |
| sinA |
| b |
| sinB |
B.在锐角△ABC中,由
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
C.在△ABC中,由acosA=bcosB,利用正弦定理可得:sin2A=sin2B,得到2A=2B或2A=2π-2B即可判断出正误;
D.在△ABC中,利用余弦定理可得:b2=a2+c2-2accosB,代入已知可得a=c,又B=60°,即可得到△ABC的形状,即可判断出正误.
解答:
解:A.在△ABC中,由正弦定理可得
=
,∴sinA>sinB?a>b?A>B,因此A>B是sinA>sinB的充要条件,正确;
B.在锐角△ABC中,A,B∈(0,
),∵A+B>
,∴
>A>
-B>0,∴sinA>sin(
-B)=cosB,因此不等式sinA>cosB恒成立,正确;
C.在△ABC中,∵acosA=bcosB,利用正弦定理可得:sinAcosA=sinBcosB,∴sin2A=sin2B,∵A,B∈(0,π),∴2A=2B或2A=2π-2B,∴A=B或A+B=
,因此
△ABC是等腰三角形或直角三角形,因此是假命题;
D.在△ABC中,若B=60°,b2=ac,由余弦定理可得:b2=a2+c2-2accosB,∴ac=a2+c2-ac,即(a-c)2=0,解得a=c,又B=60°,
∴△ABC必是等边三角形,正确.
综上可得:C是假命题.
故选:C.
| a |
| sinA |
| b |
| sinB |
B.在锐角△ABC中,A,B∈(0,
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
C.在△ABC中,∵acosA=bcosB,利用正弦定理可得:sinAcosA=sinBcosB,∴sin2A=sin2B,∵A,B∈(0,π),∴2A=2B或2A=2π-2B,∴A=B或A+B=
| π |
| 2 |
△ABC是等腰三角形或直角三角形,因此是假命题;
D.在△ABC中,若B=60°,b2=ac,由余弦定理可得:b2=a2+c2-2accosB,∴ac=a2+c2-ac,即(a-c)2=0,解得a=c,又B=60°,
∴△ABC必是等边三角形,正确.
综上可得:C是假命题.
故选:C.
点评:本题考查了正弦定理余弦定理解三角形、三角函数的单调性、诱导公式、简易逻辑的判定,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若变量x、y满足约束条件
,则z=x+y的取值范围是( )
|
| A、[4,7] | ||
| B、[-1,7] | ||
C、[
| ||
| D、[1,7] |
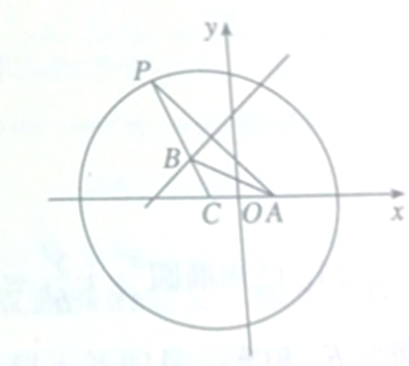 如图,已知点A的坐标为(1,0),点P为圆(x+1)2+y2=16上任意一点,点C为圆心,线段PA的垂直平分线交PC于点B.
如图,已知点A的坐标为(1,0),点P为圆(x+1)2+y2=16上任意一点,点C为圆心,线段PA的垂直平分线交PC于点B.