题目内容
在△ABC中,
(1)已知A=75°,B=45°,C=3
,求a,b.
(2)已知A=30°,B=120°,b=12,求a,c.
(1)已知A=75°,B=45°,C=3
| 2 |
(2)已知A=30°,B=120°,b=12,求a,c.
考点:正弦定理
专题:解三角形
分析:(1)由已知可求角C,由正弦定理可得:a=
,b=
,代入即可求值.
(2)由已知可求角C,由正弦定理可得:a=
,c=
,代入即可求值.
| c•sinA |
| sinC |
| c•sinB |
| sinC |
(2)由已知可求角C,由正弦定理可得:a=
| b•sinA |
| sinB |
| a•sinC |
| sinA |
解答:
解:(1)∵A=75°,B=45°,
∴C=180°-75°-45°=60°,
∴由正弦定理可得:a=
=
=3+
,b=
=
=2
.
(2)∵A=30°,B=120°,
∴C=180°-30°-120°=30°,
∴由正弦定理可得:a=
=
=4
,c=
=
=4
.
∴C=180°-75°-45°=60°,
∴由正弦定理可得:a=
| c•sinA |
| sinC |
3
| ||
| sin60° |
| 3 |
| c•sinB |
| sinC |
3
| ||
| sin60° |
| 3 |
(2)∵A=30°,B=120°,
∴C=180°-30°-120°=30°,
∴由正弦定理可得:a=
| b•sinA |
| sinB |
| 12×sin30° |
| sin120° |
| 3 |
| a•sinC |
| sinA |
4
| ||||
|
| 3 |
点评:本题主要考查了正弦定理在解三角形中的简单应用,属于基础题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
在空间直角坐标系中,点P(3,-2,1)关于x轴的对称点坐标为( )
| A、(3,2,-1) |
| B、(-3,-2,1) |
| C、(-3,2,-1) |
| D、(3,2,1) |
下列命题中,错误的是( )
| A、在△ABC中,A>B是sinA>sinB的充要条件 |
| B、在锐角△ABC中,不等式sinA>cosB恒成立 |
| C、在△ABC中,若acosA=bcosB,则△ABC必是等腰直角三角形 |
| D、在△ABC中,若B=60°,b2=ac,则△ABC必是等边三角形 |
在△ABC中,若
=
=
,则△ABC中最长的边是( )
| sinA |
| a |
| cosB |
| b |
| cosC |
| c |
| A、a | B、b | C、c | D、b或c |
若直线l1:mx-y-2=0与直线l2:(2-m)x-y+1=0互相平行,则实数m的值为( )
| A、-1 | B、0 | C、1 | D、2 |
已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=sin2x,则f(-
)=( )
| 17π |
| 6 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
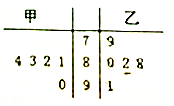 某班甲、乙两位同学升入高中以来的5次数学考试成绩的茎叶图如图,则乙同学这5次数学成绩的中位数是
某班甲、乙两位同学升入高中以来的5次数学考试成绩的茎叶图如图,则乙同学这5次数学成绩的中位数是