题目内容
求与直线y=x+3平行且与圆(x-2)2+(y-3)2=8相切的直线的方程.
考点:圆的切线方程
专题:直线与圆
分析:根据题意设切线方程,由圆心到直线的距离等于半径即可确定未知数的值,求出方程.
解答:
解:由圆得方程(x-2)2+(y-3)2=8可知,
圆心(2,3),半径2
,
设所求切线为y=x+b,即x-y+b=0,
则圆心到切线的距离为
=2
解得b=-3,或b=5,
∴所求切线方程为y=x-3,或y=x+5
圆心(2,3),半径2
| 2 |
设所求切线为y=x+b,即x-y+b=0,
则圆心到切线的距离为
| |2-3+b| | ||
|
| 2 |
解得b=-3,或b=5,
∴所求切线方程为y=x-3,或y=x+5
点评:本题考查直线与圆的位置关系,和点到直线距离公式的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数f(x)=
在[-2,2]上的最大值为2,则a的取值范围是( )
|
A、(-∞,
| ||
B、[
| ||
| C、(-∞,0) | ||
D、[0,
|
下列命题中,错误的是( )
| A、在△ABC中,A>B是sinA>sinB的充要条件 |
| B、在锐角△ABC中,不等式sinA>cosB恒成立 |
| C、在△ABC中,若acosA=bcosB,则△ABC必是等腰直角三角形 |
| D、在△ABC中,若B=60°,b2=ac,则△ABC必是等边三角形 |
已知两点A(-2,-4),B(1,5)到直线l:ax+y+1=0的距离相等,则实数a的值为( )
| A、-3 | B、3 |
| C、-3或3 | D、1或3 |
若直线l1:mx-y-2=0与直线l2:(2-m)x-y+1=0互相平行,则实数m的值为( )
| A、-1 | B、0 | C、1 | D、2 |
如图,若输入两个不同的正数,经程序运行后输出的数相同,则称这两个数为“协同数”,那么下面所给的四组数中属于“协同数”的一组是( )


| A、6,64 |
| B、8,16 |
| C、16,256 |
| D、30,512 |
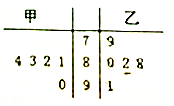 某班甲、乙两位同学升入高中以来的5次数学考试成绩的茎叶图如图,则乙同学这5次数学成绩的中位数是
某班甲、乙两位同学升入高中以来的5次数学考试成绩的茎叶图如图,则乙同学这5次数学成绩的中位数是