题目内容
求适合下列条件的双曲线的标准方程.
(1)a=6,b=3;
(2)焦点为(0,-6),(0,6),且经过点(2,-5);
(3)已知圆x2+y2-4x-9=0与y轴的两个交点A,B都在双曲线上,且A,B两点恰好将此双曲线两焦点间线段三等分.
(1)a=6,b=3;
(2)焦点为(0,-6),(0,6),且经过点(2,-5);
(3)已知圆x2+y2-4x-9=0与y轴的两个交点A,B都在双曲线上,且A,B两点恰好将此双曲线两焦点间线段三等分.
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)分类讨论,直接写出方程;
(2)求出a=2
,b=4,可得双曲线的标准方程;
(3)由已知条件推导出A(0,-3),B(0,3),从而得到a=3,2c=18,由此能求出双曲线方程.
(2)求出a=2
| 5 |
(3)由已知条件推导出A(0,-3),B(0,3),从而得到a=3,2c=18,由此能求出双曲线方程.
解答:
解:(1)焦点在x轴上的双曲线方程为
-
=1或
-
=1;
(2)c=6,
-
=1,∴a=2
,b=4,∴双曲线的标准方程为
-
=1;
(3)解方程组
,得
或
,
∵圆x2+y2-4x-9=0与y轴的两个交点A,B都在某双曲线上,
且A,B两点恰好将此双曲线的焦距三等分,
∴A(0,-3),B(0,3),
∴a=3,2c=18,∴b2=92-32=72,
∴双曲线方程为
-
=1.
| x2 |
| 36 |
| y2 |
| 9 |
| y2 |
| 36 |
| x2 |
| 9 |
(2)c=6,
| 25 |
| a2 |
| 4 |
| b2 |
| 5 |
| y2 |
| 20 |
| x2 |
| 16 |
(3)解方程组
|
|
|
∵圆x2+y2-4x-9=0与y轴的两个交点A,B都在某双曲线上,
且A,B两点恰好将此双曲线的焦距三等分,
∴A(0,-3),B(0,3),
∴a=3,2c=18,∴b2=92-32=72,
∴双曲线方程为
| y2 |
| 9 |
| x2 |
| 72 |
点评:本题考查双曲线的标准方程的求法,是基础题,解题时要认真审题,要熟练掌握双曲线的简单性质.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
设函数f(x)=
在[-2,2]上的最大值为2,则a的取值范围是( )
|
A、(-∞,
| ||
B、[
| ||
| C、(-∞,0) | ||
D、[0,
|
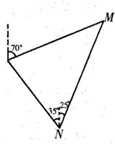 如图,一艘轮船从N处开始按照北偏西35°的方向以每小时30海里的速度航行,灯塔M原来在轮船的北偏东25°方向上,经过30分钟后,灯塔在轮船的北偏东70°方向上,则灯塔M距离N处的海里数为( )
如图,一艘轮船从N处开始按照北偏西35°的方向以每小时30海里的速度航行,灯塔M原来在轮船的北偏东25°方向上,经过30分钟后,灯塔在轮船的北偏东70°方向上,则灯塔M距离N处的海里数为( )A、
| ||||
B、
| ||||
C、30(
| ||||
D、30(
|
在空间直角坐标系中,点P(3,-2,1)关于x轴的对称点坐标为( )
| A、(3,2,-1) |
| B、(-3,-2,1) |
| C、(-3,2,-1) |
| D、(3,2,1) |
下列命题中,错误的是( )
| A、在△ABC中,A>B是sinA>sinB的充要条件 |
| B、在锐角△ABC中,不等式sinA>cosB恒成立 |
| C、在△ABC中,若acosA=bcosB,则△ABC必是等腰直角三角形 |
| D、在△ABC中,若B=60°,b2=ac,则△ABC必是等边三角形 |
若直线l1:mx-y-2=0与直线l2:(2-m)x-y+1=0互相平行,则实数m的值为( )
| A、-1 | B、0 | C、1 | D、2 |