题目内容
已知函数f（x）=2sinxcosx+2
cos2x-
．
（1）求函数f（x）的最小正周期和单调递增区间；
（2）在锐角三角形ABC中，若f（A）=1，bc=2，求△ABC的面积．
| 3 |
| 3 |
（1）求函数f（x）的最小正周期和单调递增区间；
（2）在锐角三角形ABC中，若f（A）=1，bc=2，求△ABC的面积．
考点：余弦定理,三角函数中的恒等变换应用
专题：三角函数的图像与性质,解三角形
分析：（1）由三角函数中的恒等变换应用化简函数解析式可得f（x）=2sin（2x+
），由周期公式可求T，由2kπ-
≤2x+
≤2kπ+
，k∈Z可解得函数f（x）的单调递增区间；
（2）由已知得sin（2A+
）=
，可解得：2A+
=2kπ+
，k∈Z，或2A+
=2kπ+
，k∈Z（舍去），又△ABC为锐角三角形，可得A，又bc=2，由三角形面积公式即可得解．
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
（2）由已知得sin（2A+
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
| π |
| 6 |
解答：
解：（1）∵f（x）=2sinxcosx+2
cos2x-
=sin2x+
cos2x=2sin（2x+
），
∴T=
=π，
∴由2kπ-
≤2x+
≤2kπ+
，k∈Z可解得：kπ-
≤x≤kπ+
，k∈Z，
∴函数f（x）的单调递增区间是：[kπ-
，kπ+
]，k∈Z；
（2）∵f（A）=2sin（2A+
）=1，即有：sin（2A+
）=
，
∴可解得：2A+
=2kπ+
，k∈Z，或2A+
=2kπ+
，k∈Z（舍去），
∴可解得：A=kπ+
，k∈Z，
又△ABC为锐角三角形，
则A=
，又bc=2，
则△ABC的面积S=
bcsinA=
×2×
=
．
| 3 |
| 3 |
| 3 |
| π |
| 3 |
∴T=
| 2π |
| 2 |
∴由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
∴函数f（x）的单调递增区间是：[kπ-
| 5π |
| 12 |
| π |
| 12 |
（2）∵f（A）=2sin（2A+
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
∴可解得：2A+
| π |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
| π |
| 6 |
∴可解得：A=kπ+
| π |
| 4 |
又△ABC为锐角三角形，
则A=
| π |
| 4 |
则△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
点评：本题主要考查了三角函数中的恒等变换应用，正弦函数的周期性及单调性，考查了余弦定理，三角形面积公式的应用，属于中档题．
练习册系列答案
相关题目
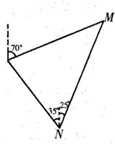如图，一艘轮船从N处开始按照北偏西35°的方向以每小时30海里的速度航行，灯塔M原来在轮船的北偏东25°方向上，经过30分钟后，灯塔在轮船的北偏东70°方向上，则灯塔M距离N处的海里数为（ ）A、
| ||||
B、
| ||||
C、30（
| ||||
D、30（
|
下列命题中，错误的是（ ）
| A、在△ABC中，A＞B是sinA＞sinB的充要条件 |
| B、在锐角△ABC中，不等式sinA＞cosB恒成立 |
| C、在△ABC中，若acosA=bcosB，则△ABC必是等腰直角三角形 |
| D、在△ABC中，若B=60°，b2=ac，则△ABC必是等边三角形 |
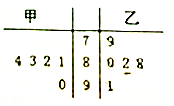某班甲、乙两位同学升入高中以来的5次数学考试成绩的茎叶图如图，则乙同学这5次数学成绩的中位数是已知两点A（-2，-4），B（1，5）到直线l：ax+y+1=0的距离相等，则实数a的值为（ ）
| A、-3 | B、3 |
| C、-3或3 | D、1或3 |