题目内容
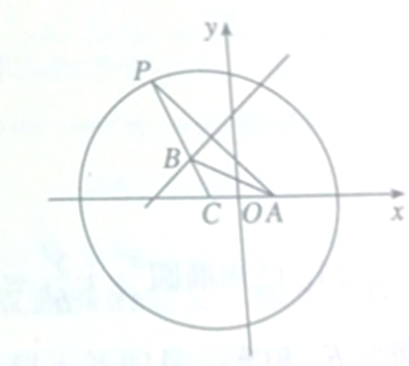 如图,已知点A的坐标为(1,0),点P为圆(x+1)2+y2=16上任意一点,点C为圆心,线段PA的垂直平分线交PC于点B.
如图,已知点A的坐标为(1,0),点P为圆(x+1)2+y2=16上任意一点,点C为圆心,线段PA的垂直平分线交PC于点B.(1)求证:△ABC的周长为定值;
(2)求点B的轨迹方程.
考点:轨迹方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)直接由题意可得△ABC的周长为|BA|+|BC|+|AC|=|CP|+CA|=4+2=6定值;
(2)|BA|+|BC|=|CP|=4>|CA|=2,点Q的轨迹是以C,A为焦点的椭圆,且得到长半轴和半焦距,再由b2=a2-c2求得b2,则点B的轨迹方程可求.
(2)|BA|+|BC|=|CP|=4>|CA|=2,点Q的轨迹是以C,A为焦点的椭圆,且得到长半轴和半焦距,再由b2=a2-c2求得b2,则点B的轨迹方程可求.
解答:
解:(1)依题意知:|BA|=|BP|,
∴△ABC的周长为|BA|+|BC|+|AC|=|CP|+CA|=4+2=6定值;
(2)|BA|+|BC|=|CP|=4>|CA|=2,
∴点Q的轨迹是以C,A为焦点的椭圆,
a=2,c=1,b2=a2-c2=3,
∴所求椭圆方程为
+
=1.
∴△ABC的周长为|BA|+|BC|+|AC|=|CP|+CA|=4+2=6定值;
(2)|BA|+|BC|=|CP|=4>|CA|=2,
∴点Q的轨迹是以C,A为焦点的椭圆,
a=2,c=1,b2=a2-c2=3,
∴所求椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
点评:本题考查了椭圆方程的求法,考查椭圆的定义,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,为了测量某湖泊两侧A,B间的距离,某同学首先选定了与A,B不共线的一点C,然后给出了四种测量方案:(△ABC的角A,B,C所对的边分别记为a,b,c)
如图所示,为了测量某湖泊两侧A,B间的距离,某同学首先选定了与A,B不共线的一点C,然后给出了四种测量方案:(△ABC的角A,B,C所对的边分别记为a,b,c)①测量A,C,b.②测量a,b,C.③测量A,B,a.④测量a,b,B.
则一定能确定A,B间距离的所有方案的序号为( )
| A、①②③ | B、②③④ |
| C、①③④ | D、①②③④ |
设函数f(x)=
在[-2,2]上的最大值为2,则a的取值范围是( )
|
A、(-∞,
| ||
B、[
| ||
| C、(-∞,0) | ||
D、[0,
|
下列命题中,错误的是( )
| A、在△ABC中,A>B是sinA>sinB的充要条件 |
| B、在锐角△ABC中,不等式sinA>cosB恒成立 |
| C、在△ABC中,若acosA=bcosB,则△ABC必是等腰直角三角形 |
| D、在△ABC中,若B=60°,b2=ac,则△ABC必是等边三角形 |