题目内容
 已知抛物线Q:y2=2px(p>0)的焦点与椭圆
已知抛物线Q:y2=2px(p>0)的焦点与椭圆| x2 |
| 4 |
| y2 |
| 3 |
(Ⅰ)求抛物线Q的方程;
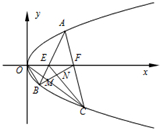
(Ⅱ)如图所示,设A、B、C是抛物线Q上任意不同的三点,且点A位于x轴上方,B、C位于x轴下方.直线AB、AC与x轴分别交于点E、F,BF与直线OC、EC分别交于点M、N.记△OBM、△ENF、△MNC的面积依次为S1、S2、S3,求证:S1+S2=S3.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)利用椭圆和抛物线的标准即可得出焦点坐标;
(II)设点A(x1,y1),B(x2,y2),C(x3,y3),E(x4,y4),F(x5,y5).要证S1+S2=S3,即证S△OBF=S△OCE,即证x5y2=x4y3,利用直线的方程与抛物线的方程联立可得根与系数,进而得到.
(II)设点A(x1,y1),B(x2,y2),C(x3,y3),E(x4,y4),F(x5,y5).要证S1+S2=S3,即证S△OBF=S△OCE,即证x5y2=x4y3,利用直线的方程与抛物线的方程联立可得根与系数,进而得到.
解答:
解:(Ⅰ)由椭圆
+
=1的方程可得a2=4,b2=3,
∴c=
=1,
∴右焦点为(1,0),
由于抛物线Q:y2=2px(p>0)的焦点与椭圆
+
=1的右焦点相同,
∴
=1,解得p=2,
故抛物线Q的方程为y2=4x;
(Ⅱ) 设点A(x1,y1),B(x2,y2),C(x3,y3),E(x4,y4),F(x5,y5).
要证S1+S2=S3,即证S△OBF=S△OCE,即证x5y2=x4y3,
设直线AB的方程为x=ty+x4,代入y2=4x得
y2-4ty-4x4=0,
由韦达定理得,y1y2=-4x4,①
同理可得y1y3=-4x5 ②
①×y3得y1y2y3=-4x4y3,②×y2得y1y2y3=-4x5y2,
∴x5y2=x4y3,证毕.
| x2 |
| 4 |
| y2 |
| 3 |
∴c=
| a2-b2 |
∴右焦点为(1,0),
由于抛物线Q:y2=2px(p>0)的焦点与椭圆
| x2 |
| 4 |
| y2 |
| 3 |
∴
| p |
| 2 |
故抛物线Q的方程为y2=4x;
(Ⅱ) 设点A(x1,y1),B(x2,y2),C(x3,y3),E(x4,y4),F(x5,y5).
要证S1+S2=S3,即证S△OBF=S△OCE,即证x5y2=x4y3,
设直线AB的方程为x=ty+x4,代入y2=4x得
y2-4ty-4x4=0,
由韦达定理得,y1y2=-4x4,①
同理可得y1y3=-4x5 ②
①×y3得y1y2y3=-4x4y3,②×y2得y1y2y3=-4x5y2,
∴x5y2=x4y3,证毕.
点评:本题考查了椭圆与抛物线的标准方程及其性质、直线与抛物线相交问题转化为方程联立得到根与系数的关系、面积问题的转化等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
某校共有学生2000名,各年级男、女学生人数如表,现用分层抽样的方法在全校学生中抽取64人,则应在三年级抽取的学生人数为( )
| 一年级 | 二年级 | 三年级 | |
| 女生 | 385 | 380 | b |
| 男生 | 375 | 360 | c |
| A、19 | B、16 | C、500 | D、18 |
若实数x,y满足不等式组
,则|x+y|的最小值为( )
|
| A、3 | B、-1 | C、1 | D、2 |
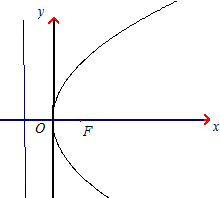 已知抛物线y2=2px(p>0),其焦点为F,一条过焦点F,倾斜角为θ(0<θ<π)的直线交抛物线于A,B两点,连接AO(O为坐标原点),交准线于点B',连接BO,交准线于点A',求四边形ABB'A'的面积.
已知抛物线y2=2px(p>0),其焦点为F,一条过焦点F,倾斜角为θ(0<θ<π)的直线交抛物线于A,B两点,连接AO(O为坐标原点),交准线于点B',连接BO,交准线于点A',求四边形ABB'A'的面积.