题目内容
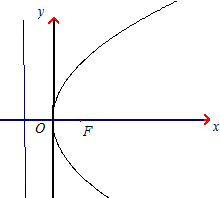 已知抛物线y2=2px(p>0),其焦点为F,一条过焦点F,倾斜角为θ(0<θ<π)的直线交抛物线于A,B两点,连接AO(O为坐标原点),交准线于点B',连接BO,交准线于点A',求四边形ABB'A'的面积.
已知抛物线y2=2px(p>0),其焦点为F,一条过焦点F,倾斜角为θ(0<θ<π)的直线交抛物线于A,B两点,连接AO(O为坐标原点),交准线于点B',连接BO,交准线于点A',求四边形ABB'A'的面积.考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:分类讨论,当θ=
时,SABB′A′=2p2;当θ≠
时,令k=tanθ,证明四边形ABB'A'是直角梯形,利用SABB′A′=
(|AA′|+|BB′|)•|A′B′|=
|AB|•|A′B′|,可求四边形ABB'A'的面积.
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
 解:当θ=
解:当θ=
时,SABB′A′=2p2. …(4分)
当θ≠
时,令k=tanθ.
设A(x1,y1),B(x2,y2),则
由y=k(x-
),①y2=2px,②
消去x得,y2-
y-p2=0,
所以y1+y2=
,y1y2=-p2. ③
又直线AO的方程为:y=
x,即为y=
x,
所以,AO与准线的交点的坐标为B′(-
,-
),
而由③知,y2=-
,
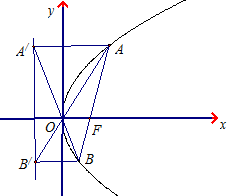
所以B和B'的纵坐标相等,从而BB'∥x轴.
同理AA'∥x轴,故四边形ABB'A'是直角梯形.…(9分)
所以,它的面积为SABB′A′=
(|AA′|+|BB′|)•|A′B′|=
|AB|•|A′B′|
=
•|y2-y1|=
(y2-y1)2
=
[(y1+y2)2-4y1y2]
=2p2(1+
)
=2p2(1+cot2θ)
.…(14分)
 解:当θ=
解:当θ=| π |
| 2 |
当θ≠
| π |
| 2 |
设A(x1,y1),B(x2,y2),则
由y=k(x-
| p |
| 2 |
消去x得,y2-
| 2p |
| k |
所以y1+y2=
| 2p |
| k |
又直线AO的方程为:y=
| y1 |
| x1 |
| 2p |
| y1 |
所以,AO与准线的交点的坐标为B′(-
| p |
| 2 |
| p2 |
| y1 |
而由③知,y2=-
| p2 |
| y1 |
所以B和B'的纵坐标相等,从而BB'∥x轴.
同理AA'∥x轴,故四边形ABB'A'是直角梯形.…(9分)
所以,它的面积为SABB′A′=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| (x2-x1)2+(y2-y1)2 |
| 1 |
| 2 |
1+
|
| 1 |
| 2 |
1+
|
=2p2(1+
| 1 |
| k2 |
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查直线与抛物线的位置关系,考查四边形面积的计算,考查学生的计算能力,考查分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
过点A(23,2)作圆(x+1)2+(y-2)2=625的弦,其中弦长为整数的条数为( )
| A、36 | B、37 | C、72 | D、74 |
若x<0,则2+3x+
的最大值是( )
| 4 |
| x |
A、2+4
| ||
B、2±4
| ||
C、2-4
| ||
| D、以上都不对 |
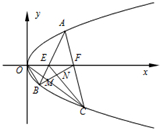 已知抛物线Q:y2=2px(p>0)的焦点与椭圆
已知抛物线Q:y2=2px(p>0)的焦点与椭圆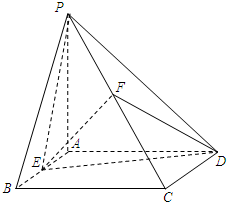 如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD.△PAD为等腰直角三角形,且PA⊥AD. E,F分别为底边AB和侧棱PC的中点.
如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD.△PAD为等腰直角三角形,且PA⊥AD. E,F分别为底边AB和侧棱PC的中点.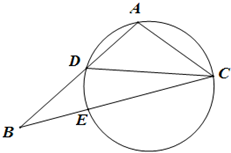 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=2,AB=3,EC=
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=2,AB=3,EC=