题目内容
已知函数f(x)=2sinaxcosax+2
cos2ax-
(其中a>0),点A,B是y=f(x)图象上相邻的两个最值点,且|AB|=
.
(1)求函数f(x)的解析式;
(2)在锐角三角形△ABC中,f(A)=0,BC=
,AB=3,求AC的长.
| 3 |
| 3 |
|
(1)求函数f(x)的解析式;
(2)在锐角三角形△ABC中,f(A)=0,BC=
| 13 |
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:(1)f(x)解析式利用二倍角的正弦、余弦函数公式化简,整理后再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据|AB|的值,求出f(x)的周期T,利用周期公式即可求出a的值,确定出f(x)解析式;
(2)由f(x)解析式,以及f(A)=0,求出A的度数,再由BC,AB的长,利用余弦定理即可求出AC的长.
(2)由f(x)解析式,以及f(A)=0,求出A的度数,再由BC,AB的长,利用余弦定理即可求出AC的长.
解答:
解:(1)f(x)=2sinaxcosax+
(2cos2ax-1)=sin2ax+
cos2ax=2sin(2ax+
),
设函数f(x)的最小正周期为T,
由题意得:|AB|=
=
,解得:T=π,
∴
=π,解得:a=1,
则f(x)=2sin(2x+
);
(2)∵f(A)=2sin(2A+
)=0,
∴2A+
=kπ,k∈Z,
又0<A<
,
∴A=
,
由余弦定理,得BC2=AB2+AC2-2AB•ACcosA,
又BC=
,AB=3,
∴13=9+AC2-2×3×AC×
,
解得:AC=4.
| 3 |
| 3 |
| π |
| 3 |
设函数f(x)的最小正周期为T,
由题意得:|AB|=
42+(
|
|
∴
| 2π |
| 2a |
则f(x)=2sin(2x+
| π |
| 3 |
(2)∵f(A)=2sin(2A+
| π |
| 3 |
∴2A+
| π |
| 3 |
又0<A<
| π |
| 2 |
∴A=
| π |
| 3 |
由余弦定理,得BC2=AB2+AC2-2AB•ACcosA,
又BC=
| 13 |
∴13=9+AC2-2×3×AC×
| 1 |
| 2 |
解得:AC=4.
点评:此题考查了余弦定理,三角形的周期性及其求法,二倍角的正弦、余弦函数公式,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
执行如图所示的程序框图,输入m=828,n=345,则输出的实数m的值是( )


| A、68 | B、69 |
| C、138 | D、139 |
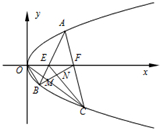 已知抛物线Q:y2=2px(p>0)的焦点与椭圆
已知抛物线Q:y2=2px(p>0)的焦点与椭圆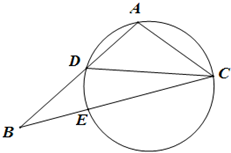 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=2,AB=3,EC=
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=2,AB=3,EC=