题目内容
圆C1:x2+y2+2x+8y-8=0与圆C2:x2+y2-4x-4y-2=0的公共弦长等于 .
考点:直线与圆相交的性质
专题:直线与圆
分析:将两圆方程化为标准方程,找出圆心C1坐标,半径r1=5,圆心C2坐标,半径r2,利用两点间的距离公式求出C1C2的长,Rt△AC1D中,利用勾股定理表示出C1D,同理表示出C2D=
,由C1D+DC2=C1C2列出关于AD的方程,求出方程的解即可得到AD的长,进而确定出AB的长.
| 10-AD2 |
解答:
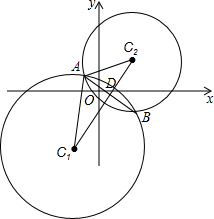 解:将两圆方程化为标准方程得:(x+1)2+(y+4)2=25,(x-2)2+(y-2)2=10,
解:将两圆方程化为标准方程得:(x+1)2+(y+4)2=25,(x-2)2+(y-2)2=10,
∴圆心C1(-1,-4),半径r1=5,圆心C2(2,2),半径r2=
,
∴C1C2=
=3
,
∵C1C2⊥AB,
∴D为AB的中点,即AD=BD=
AB,
在Rt△AC1D中,C1D=
,
同理C2D=
,
∴C1D+DC2=C1C2,即
+
=3
,
解得:AD=
,
则AB=2AD=2
.
故答案为:2
 解:将两圆方程化为标准方程得:(x+1)2+(y+4)2=25,(x-2)2+(y-2)2=10,
解:将两圆方程化为标准方程得:(x+1)2+(y+4)2=25,(x-2)2+(y-2)2=10,∴圆心C1(-1,-4),半径r1=5,圆心C2(2,2),半径r2=
| 10 |
∴C1C2=
| (-1-2)2+(-4-2)2 |
| 5 |
∵C1C2⊥AB,
∴D为AB的中点,即AD=BD=
| 1 |
| 2 |
在Rt△AC1D中,C1D=
| 25-AD2 |
同理C2D=
| 10-AD2 |
∴C1D+DC2=C1C2,即
| 25-AD2 |
| 10-AD2 |
| 5 |
解得:AD=
| 5 |
则AB=2AD=2
| 5 |
故答案为:2
| 5 |
点评:此题考查了直线与圆相交的性质,涉及的知识有:垂径定理,勾股定理,圆的标准方程,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
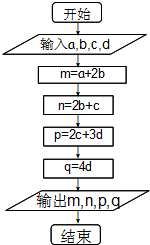 为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则如图所示,例如明文1,2,3,4,对应密文5,7,18,16.当对方收到密文14,9,23,28时,则解密得到的明文为( )
为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则如图所示,例如明文1,2,3,4,对应密文5,7,18,16.当对方收到密文14,9,23,28时,则解密得到的明文为( )| A、4,6,1,7 |
| B、6,4,1,7 |
| C、1,6,4,7 |
| D、7,6,1,4 |
过点A(23,2)作圆(x+1)2+(y-2)2=625的弦,其中弦长为整数的条数为( )
| A、36 | B、37 | C、72 | D、74 |
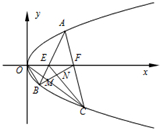 已知抛物线Q:y2=2px(p>0)的焦点与椭圆
已知抛物线Q:y2=2px(p>0)的焦点与椭圆