题目内容
已知函数f(x)=lnx-x+1,x∈(0,+∞),g(x)=x3-ax.
(1)求f(x)的最大值;
(2)若对?x1∈(0,+∞),总存在x2∈[1,2]使得f(x1)≤g(x2)成立,求a的取值范围;
(3)证明不等式:(
)n+(
)n+…+(
)n<
.
(1)求f(x)的最大值;
(2)若对?x1∈(0,+∞),总存在x2∈[1,2]使得f(x1)≤g(x2)成立,求a的取值范围;
(3)证明不等式:(
| 1 |
| n |
| 2 |
| n |
| n |
| n |
| e |
| e-1 |
考点:导数在最大值、最小值问题中的应用,不等式的证明
专题:综合题,导数的综合应用
分析:(1)求导函数,确定函数的单调性,可得f(x)≤f(1)=0,从而可求f(x)的最大值;
(2)若对?x1∈(0,+∞),总存在x2∈[1,2]使得f(x1)≤g(x2)成立,等价于f(x)max≤g(x)max,
由(1)知f(x)max=0,分类讨论,求出g(x)max,即可求a的取值范围;
(3)由(1)知f(x)≤0即lnx≤x-1(x>0),取x=
,可得ln
≤
-1=
,从而可得(
)n≤ek-n,即可证明结论.
(2)若对?x1∈(0,+∞),总存在x2∈[1,2]使得f(x1)≤g(x2)成立,等价于f(x)max≤g(x)max,
由(1)知f(x)max=0,分类讨论,求出g(x)max,即可求a的取值范围;
(3)由(1)知f(x)≤0即lnx≤x-1(x>0),取x=
| k |
| n |
| k |
| n |
| k |
| n |
| k-n |
| n |
| k |
| n |
解答:
(1)解:∵f(x)=lnx-x+1 (x>0)
∴f′(x)=
,
∴当0<x<1时,f′(x)>0,x>1时,f′(x)<0,
∴f(x)≤f(1)=0,∴f(x)的最大值为0;
(2)解:?x1∈(0,+∞),总存在x2∈[1,2]使得f(x1)≤g(x2)成立,
等价于f(x)max≤g(x)max,
由(1)知f(x)max=0,
当a≤0时,g(x)=x3-ax在x∈[1,2]时恒为正,满足题意.
当a>0时,g′(x)=3x2-a,
令g′(x)=0,解得x=±
,
∴g(x)在(-∞,-
),(
,+∞)上单调增
若
≤1即0<a≤3时,g(x)max=g(2)=8-2a,∴8-2a≥0,∴a≤4,∴0<a≤3
若1<
≤2即3<a≤12时,g(x)在[1,
],[
,2]
而g(1)=1-a<0,g(2)=8-2a在(3,4]为正,在(4,12)为负
∴3<a≤4
当
>2而a>12时g(1)<0,g(2)<0不合题意
综上a的取值范围为 a≤4.
(3)证明:由(1)知f(x)≤0即lnx≤x-1(x>0)
取x=
,∴ln
≤
-1=
,
∴nln
≤k-n,即(
)n≤ek-n,
∴(
)n+(
)n+…+(
)n≤e1-n+e2-n+…+en-n=
=
<
.
∴f′(x)=
| 1-x |
| x |
∴当0<x<1时,f′(x)>0,x>1时,f′(x)<0,
∴f(x)≤f(1)=0,∴f(x)的最大值为0;
(2)解:?x1∈(0,+∞),总存在x2∈[1,2]使得f(x1)≤g(x2)成立,
等价于f(x)max≤g(x)max,
由(1)知f(x)max=0,
当a≤0时,g(x)=x3-ax在x∈[1,2]时恒为正,满足题意.
当a>0时,g′(x)=3x2-a,
令g′(x)=0,解得x=±
|
∴g(x)在(-∞,-
|
|
若
|
若1<
|
|
|
而g(1)=1-a<0,g(2)=8-2a在(3,4]为正,在(4,12)为负
∴3<a≤4
当
|
综上a的取值范围为 a≤4.
(3)证明:由(1)知f(x)≤0即lnx≤x-1(x>0)
取x=
| k |
| n |
| k |
| n |
| k |
| n |
| k-n |
| n |
∴nln
| k |
| n |
| k |
| n |
∴(
| 1 |
| n |
| 2 |
| n |
| n |
| n |
| e1-n-en-n•e |
| 1-e |
| e-e1-n |
| e-1 |
| e |
| e-1 |
点评:本题考查导数知识的运用,考查函数的最值,考查不等式的证明,考查分类讨论的数学思想,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知等差数列{an}中,a7=
,则a6+a7+a8等于( )
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
| D、111 |
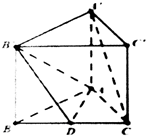 如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2
如图,正三棱柱ABC-A′B′C′中,D是BC的中点,AA′=AB=2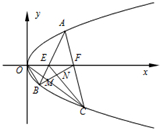 已知抛物线Q:y2=2px(p>0)的焦点与椭圆
已知抛物线Q:y2=2px(p>0)的焦点与椭圆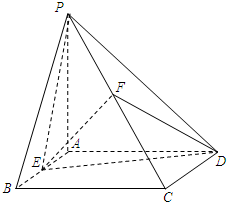 如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD.△PAD为等腰直角三角形,且PA⊥AD. E,F分别为底边AB和侧棱PC的中点.
如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD.△PAD为等腰直角三角形,且PA⊥AD. E,F分别为底边AB和侧棱PC的中点.