题目内容
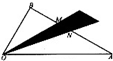 如图,己知|
如图,己知|| OA |
| OB |
| OP |
| OA |
| OB |
①x≥0,y≥0;②x-y≥0;③x-y≤0;④x-2y≥0;⑤2x-y≥0.
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:利用向量共线定理,及三角形法则,将向量
用
,
表示出来,则
,
的系数对应等于x,y.由此即可解题.
| OP |
| OA |
| OB |
| OA |
| OB |
解答:
解:设线段OP与AB的交点为C,
则由向量共线定理知:存在实数λ,使得
=λ
其中λ>0,
∴
=λ
=λ(
+
)
=λ
+λ
.
∵
,
共线,
∴存在实数μ,使得
=μ
,
∵N为BC的中点,
∴μ>
;
又∵|
|=2,|
|=1,OM平分∠AOB,
∴由正弦定理知,AM=2BM,
∴AC≤AM=
AB,
故
≤μ≤
,
∴
=λ
+λμ
=λ
+λμ(
-
)
=λ(1-μ)
+λμ
,
∴x=λ(1-μ),y=λμ
又∵λ>0,
≤μ≤
,
∴x≥0,y≥0;
x-y=λ(1-2μ)≤0;
2x-y=λ(2-3μ)≥0.
故答案为:①③⑤.
则由向量共线定理知:存在实数λ,使得
| OP |
| OC |
∴
| OP |
| OC |
=λ(
| OA |
| AC |
=λ
| OA |
| AC |
∵
| AC |
| AB |
∴存在实数μ,使得
| AC |
| AB |
∵N为BC的中点,
∴μ>
| 1 |
| 2 |
又∵|
| OA |
| OB |
∴由正弦定理知,AM=2BM,
∴AC≤AM=
| 2 |
| 3 |
故
| 1 |
| 2 |
| 2 |
| 3 |
∴
| OP |
| OA |
| AB |
=λ
| OA |
| OB |
| OA |
=λ(1-μ)
| OA |
| OB |
∴x=λ(1-μ),y=λμ
又∵λ>0,
| 1 |
| 2 |
| 2 |
| 3 |
∴x≥0,y≥0;
x-y=λ(1-2μ)≤0;
2x-y=λ(2-3μ)≥0.
故答案为:①③⑤.
点评:本题主要考察了平面向量的共线定理以及向量的三角形法则,并涉及到了正弦定理,难度较大,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某程序框图如图,则该程序运行后输出的值为( )


| A、6 | B、7 | C、8 | D、9 |