题目内容
椭圆C:
+
=1(a>b>0)的左、右焦点分别是F1,F2,离心率为
,过F1且垂直于x轴的直线被椭圆C截得的线段长为l
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点,设直线PF1,PF2的斜率分别为k1,k2,若k≠0,试证明:
+
为定值,并求出这个定值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点,设直线PF1,PF2的斜率分别为k1,k2,若k≠0,试证明:
| 1 |
| kk1 |
| 1 |
| kk2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出
=1,
=
,由此能求出椭圆C的方程.
(2)设P(x0,y0)(y0≠0),则直线l的方程为y-y0=k(x-x0).联立
,得(1+4k2)x2+8(ky0-k2x0)x+4(y02-2kx0y0+k2x02-1)=0.由此利用根的判别式结合题设条件能证明
+
为定值-8.
| 2b2 |
| a |
| c |
| a |
| ||
| 2 |
(2)设P(x0,y0)(y0≠0),则直线l的方程为y-y0=k(x-x0).联立
|
| 1 |
| kk1 |
| 1 |
| kk2 |
解答:
(1)解:∵c2=a2-b2,∴将x=-c代入椭圆方程
+
=1,得y=±
.
∵过F1且垂直于x轴的直线被椭圆C截得的线段长为l,
∴
=1,即a=2b2.…(2分)
∵离心率e=
=
,…(4分)
∴a=2,b=1.…(5分)
∴椭圆C的方程为
+y2=1.…(6分)
(2)证明:设P(x0,y0)(y0≠0),则直线l的方程为y-y0=k(x-x0).
联立
,…(8分)
整理得(1+4k2)x2+8(ky0-k2x0)x+4(y02-2kx0y0+k2x02-1)=0.
由题意知△=0,即(4-x02)k2+2x0y0k+1-y02=0.…(10分)
又
+y02=1,
∴16y02k2+8x0y0k+x02=0,
∴k=-
.…(12分)
由(2)知
+
=
+
=
,…(15分)
∴
+
=
(
+
)=(
)•
=-8,
∴
+
为定值,这个定值为-8.…(16分)
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
∵过F1且垂直于x轴的直线被椭圆C截得的线段长为l,
∴
| 2b2 |
| a |
∵离心率e=
| c |
| a |
| ||
| 2 |
∴a=2,b=1.…(5分)
∴椭圆C的方程为
| x2 |
| 4 |
(2)证明:设P(x0,y0)(y0≠0),则直线l的方程为y-y0=k(x-x0).
联立
|
整理得(1+4k2)x2+8(ky0-k2x0)x+4(y02-2kx0y0+k2x02-1)=0.
由题意知△=0,即(4-x02)k2+2x0y0k+1-y02=0.…(10分)
又
| x02 |
| 4 |
∴16y02k2+8x0y0k+x02=0,
∴k=-
| x0 |
| 4y0 |
由(2)知
| 1 |
| k1 |
| 1 |
| k2 |
x0+
| ||
| y0 |
x0-
| ||
| y0 |
| 2x0 |
| y0 |
∴
| 1 |
| kk1 |
| 1 |
| kk2 |
| 1 |
| k |
| 1 |
| k1 |
| 1 |
| k2 |
| -4y0 |
| x0 |
| 2x0 |
| y0 |
∴
| 1 |
| kk1 |
| 1 |
| kk2 |
点评:本题考查椭圆方程的求法,考查两数和为定值的证明与求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
已知集合M={x|-1<x<1},N={x|3x>1},则M∩N=( )
| A、∅ |
| B、{x|x>0} |
| C、{x|x<1} |
| D、{x|0<x<1} |
已知点P为三棱锥O-ABC的底面ABC所在平面内的一点,且
=
+k
-
,则实数k的值为( )
| OP |
| 1 |
| 2 |
| OA |
| OB |
| OC |
A、-
| ||
B、
| ||
| C、1 | ||
D、
|
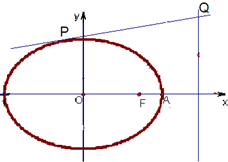 已知椭圆C:
已知椭圆C: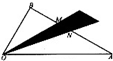 如图,己知
如图,己知