题目内容
设不等式组
表示的平面区域为M,不等式组
表示的平面区域为N.在M内随机取一个点,这个点在N内的概率的最大值是 .
|
|
考点:几何概型
专题:概率与统计
分析:根据基本不等式的性质求出平面区域N的面积的最大值,利用几何概型的概率公式即可得到结论.
解答:
解:不等式组
表示的平面区域为矩形,要使根式有意义,则1-t2≥0,即0≤t≤1,
则对应的矩形面积为2t•
≤t2+1-t2=1当且仅当t=
,即t2=
,
即t=
时取等号,此时区域N的最大面积为1,
∴在M内随机取一个点,这个点在N内的概率的最大值是
=
,
故答案为:
|
则对应的矩形面积为2t•
| 1-t2 |
| 1-t2 |
| 1 |
| 2 |
即t=
| ||
| 2 |

∴在M内随机取一个点,这个点在N内的概率的最大值是
| 1 | ||
|
| 2 |
| π |
故答案为:
| 2 |
| π |
点评:本题主要考查几何概型的概率计算,根据基本不等式的性质求出区域N的最大值是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知不等式
>0的解集为(-1,2),则二项式(ax-
)6展开式的常数项是( )
| x-2 |
| ax-1 |
| 1 |
| x2 |
| A、-15 | B、15 | C、-5 | D、5 |
在锐角△ABC中,AB=3,AC=4,其面积S△ABC=3
,则BC=( )
| 3 |
| A、5 | ||||
B、
| ||||
C、
| ||||
D、
|
 如图,己知
如图,己知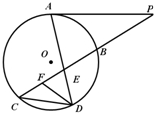 如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=
如图所示,已知PA与⊙O相切,A为切点,过点P的割线交圆于B、C两点,弦CD∥AP,AD、BC相交于点E,F为CE上一点,且∠EDF=∠C,若CE:BE=3:2,DE=3,EF=2.则PA=