题目内容
函数f(x)=
(ax+a-x)(a>0,且a≠1)的图象经过点(2,
).
(1)求f(x)的解析式;
(2)证明f(x)在[0,+∞)上是增函数.
| 1 |
| 2 |
| 41 |
| 9 |
(1)求f(x)的解析式;
(2)证明f(x)在[0,+∞)上是增函数.
考点:函数单调性的判断与证明
专题:证明题,函数的性质及应用
分析:(1)应用代入法,求出a,从而得出函数f(x)的解析式;
(2)运用函数单调性定义证明:分设值、作差、变形、定符号、下结论几步.
(2)运用函数单调性定义证明:分设值、作差、变形、定符号、下结论几步.
解答:
解:(1)∵f(x)图象过点(2,
),
∴f(2)=
,即
(a2+a-2)=
,
∴a2=9或a2=
,
∵a>0且a≠1,
∴a=3或a=
,
∴f(x)的解析式为:f(x)=
(3x+3-x);
(2)证明:设0≤x1<x2,则
f(x1)-f(x2)=
(3x1+3-x1)-
(3x2+3-x2)
=
[(3x1-3x2)+
]
=
(3x1-3x2)•
,
∵x1<x2,
∴3x1<3x2即3x1-3x2<0,
∵0≤x1<x2,
∴3x1+x2>1,即3x1+x2-1>0,3x1+x2>0,
∴f(x1)-f(x2)<0即f(x1)<f(x2),
∴f(x)在[0,+∞)上是增函数.
| 41 |
| 9 |
∴f(2)=
| 41 |
| 9 |
| 1 |
| 2 |
| 41 |
| 9 |
∴a2=9或a2=
| 1 |
| 9 |
∵a>0且a≠1,
∴a=3或a=
| 1 |
| 3 |
∴f(x)的解析式为:f(x)=
| 1 |
| 2 |
(2)证明:设0≤x1<x2,则
f(x1)-f(x2)=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3x2-3x1 |
| 3x1•3x2 |
=
| 1 |
| 2 |
| 3x1+x2-1 |
| 3x1+x2 |
∵x1<x2,
∴3x1<3x2即3x1-3x2<0,
∵0≤x1<x2,
∴3x1+x2>1,即3x1+x2-1>0,3x1+x2>0,
∴f(x1)-f(x2)<0即f(x1)<f(x2),
∴f(x)在[0,+∞)上是增函数.
点评:本题主要考查函数的单调性的证明,解题时必须严格按照五个步骤加以证明,特别注意三、四两个步骤.本题是一道基础题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
已知点P为三棱锥O-ABC的底面ABC所在平面内的一点,且
=
+k
-
,则实数k的值为( )
| OP |
| 1 |
| 2 |
| OA |
| OB |
| OC |
A、-
| ||
B、
| ||
| C、1 | ||
D、
|
已知不等式
>0的解集为(-1,2),则二项式(ax-
)6展开式的常数项是( )
| x-2 |
| ax-1 |
| 1 |
| x2 |
| A、-15 | B、15 | C、-5 | D、5 |
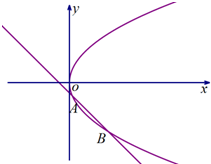 已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点.
已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点.
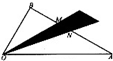 如图,己知
如图,己知