题目内容
实数x、y满足x2+y2=4,则x+y-xy的最大值为 .
考点:基本不等式
专题:三角函数的图像与性质
分析:由实数x、y满足x2+y2=4,利用三角函数代换x=2cosθ,y=2sinθ.令t=sinθ+cosθ=
sin(θ+
)(θ∈[0,2π)),t∈[-
,
],可得2sinθcosθ=t2-1.x+y-xy=2cosθ+2sinθ-4sinθcosθ=-2(t-
)2+
,再利用二次函数的单调性即可得出.
| 2 |
| π |
| 4 |
| 2 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解答:
解:∵实数x、y满足x2+y2=4,
∴可设x=2cosθ,y=2sinθ.
令t=sinθ+cosθ=
sin(θ+
)(θ∈[0,2π)),
∴t∈[-
,
].
则t2=1+2sinθcosθ,可得2sinθcosθ=t2-1.
∴x+y-xy=2cosθ+2sinθ-4sinθcosθ
=2t-2(t2-1)
=-2(t-
)2+
≤
,
当且仅当t=
时,x+y-xy取得最大值为
.
故答案为:
.
∴可设x=2cosθ,y=2sinθ.
令t=sinθ+cosθ=
| 2 |
| π |
| 4 |
∴t∈[-
| 2 |
| 2 |
则t2=1+2sinθcosθ,可得2sinθcosθ=t2-1.
∴x+y-xy=2cosθ+2sinθ-4sinθcosθ
=2t-2(t2-1)
=-2(t-
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
当且仅当t=
| 1 |
| 2 |
| 5 |
| 2 |
故答案为:
| 5 |
| 2 |
点评:本题考查了圆的参数方程、三角函数代换、三角函数基本关系式、二次函数的单调性等基础知识与基本技能方法,考查了转化方法和计算能力,属于中档题.

练习册系列答案
相关题目
在锐角△ABC中,AB=3,AC=4,其面积S△ABC=3
,则BC=( )
| 3 |
| A、5 | ||||
B、
| ||||
C、
| ||||
D、
|
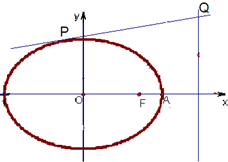 已知椭圆C:
已知椭圆C: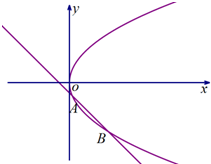 已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点.
已知抛物线C:y2=4x,直线l:y=-x+b与抛物线C交于A,B两点.
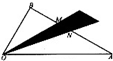 如图,己知
如图,己知