题目内容
已知函数f（x）=log
[（a-1）x-2]．
（1）若a＞1，求f（x）的定义域；
（2）若f（x）＞0在[1，
]上恒成立，求实数a的取值范围．
| 1 |
| a |
（1）若a＞1，求f（x）的定义域；
（2）若f（x）＞0在[1，
| 5 |
| 4 |
考点：对数函数图象与性质的综合应用
专题：函数的性质及应用
分析：（1）根据对数函数真数大于0，底数大于0，解得即可．
（2）利用分类讨论的思想，分a＞1和0＜a＜1，两种情况，利用函数的单调性求得．
（2）利用分类讨论的思想，分a＞1和0＜a＜1，两种情况，利用函数的单调性求得．
解答：
解（1）：由a＞1，a-1＞0，解（a-1）x-2＞0得x＞
∴f（x）的定义域是（
，+∞）
（2）：①若a＞1，则0＜
＜1，即在[1，
]上恒有0＜（a-1）x-2＜1
∵a-1＞0，
∴（a-1）x-2为单调增函数，只要
，
∴3＜a＜
②若0＜a＜1，则
＞1，即在[1，
]上恒有（a-1）x-2＞1
∵a-1＜0，
∴（a-1）x-2为单调减函数，只要（a-1）×
-2＞1，
∴a＞
∵0＜a＜1，∴a∈∅
综上，a 的取值范围为（3，
）
| 2 |
| a-1 |
∴f（x）的定义域是（
| 2 |
| a-1 |
（2）：①若a＞1，则0＜
| 1 |
| a |
| 5 |
| 4 |
∵a-1＞0，
∴（a-1）x-2为单调增函数，只要
|
∴3＜a＜
| 17 |
| 5 |
②若0＜a＜1，则
| 1 |
| a |
| 5 |
| 4 |
∵a-1＜0，
∴（a-1）x-2为单调减函数，只要（a-1）×
| 5 |
| 4 |
∴a＞
| 17 |
| 5 |
∵0＜a＜1，∴a∈∅
综上，a 的取值范围为（3，
| 17 |
| 5 |
点评：本题主要考查了对数函数性质，和利用单调性求参数的取值范围，关键是分类思想．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
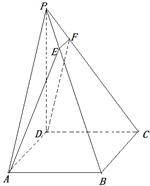如图，已知ABCD是正方形，PD⊥平面ABCD，
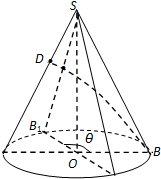如图已知圆锥SO的底面半径为4，母线长为8，三角形SAB是圆锥的一个轴截面，D是SA上的一点，且
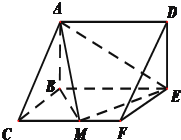已知：直三棱柱ABC-DEF中，