题目内容
学校从参加高一年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及各组频数如下:[40,50),2;[50,60),3;[60,70),14;[70,80),15;[80,90),12;[90,100],4.
(1)在给出的样本频率分布表中,求A,B,C,D的值;
(2)估计成绩在80分以上(含80分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在[90,100]的学生中选两位同学,共同帮助成绩在[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.
样本频率分布表:
(1)在给出的样本频率分布表中,求A,B,C,D的值;
(2)估计成绩在80分以上(含80分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在[90,100]的学生中选两位同学,共同帮助成绩在[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.
样本频率分布表:
| 分组 | 频数 | 频率 |
| [40,50) | 2 | 0.04 |
| [50,60) | 3 | 0.06 |
| [60,70) | 14 | 0.28 |
| [70,80) | 15 | 0.30 |
| [80,90) | A | B |
| [90,100] | 4 | 0.08 |
| 合计 | C | D |
考点:频率分布表
专题:计算题,概率与统计
分析:(1)根据题意可知A、B、C、D的值;
(2)求得[80,90)和[90,100]两组数据的频率之和,可得成绩在80分以上(含80分)学生的比例;
(3)根据成绩在[90,100]和[40,50)的学生数,分别求出实行“二帮一”小组的所有情形数及甲、乙两同学恰好被安排在同一小组的情形数,代入古典概型概率公式计算.
(2)求得[80,90)和[90,100]两组数据的频率之和,可得成绩在80分以上(含80分)学生的比例;
(3)根据成绩在[90,100]和[40,50)的学生数,分别求出实行“二帮一”小组的所有情形数及甲、乙两同学恰好被安排在同一小组的情形数,代入古典概型概率公式计算.
解答:
解:(1)由题意知:A=12; B=0.24; C=50; D=1;
(2)估计成绩在80分以上(含80分)的数据包括[80,90)和[90,100]两组数据,
两组数据的频率之和为0.24+0.08=0.32,
∴成绩在80分以上(含80分)学生的比例为32%;
(3)成绩在[90,100]的学生有4人,成绩在[40,50)的学生有2人,
实行“二帮一”小组,共有
=12种情形,
其中甲、乙两同学恰好被安排在同一小组的有
=3种情形,
∴甲、乙两同学恰好被安排在同一小组的概率为
=
.
(2)估计成绩在80分以上(含80分)的数据包括[80,90)和[90,100]两组数据,
两组数据的频率之和为0.24+0.08=0.32,
∴成绩在80分以上(含80分)学生的比例为32%;
(3)成绩在[90,100]的学生有4人,成绩在[40,50)的学生有2人,
实行“二帮一”小组,共有
| C | 2 4 |
| ×C | 1 2 |
其中甲、乙两同学恰好被安排在同一小组的有
| C | 1 3 |
∴甲、乙两同学恰好被安排在同一小组的概率为
| 3 |
| 12 |
| 1 |
| 4 |
点评:本题考查了由频率分布表求频率,考查了古典概型的概率计算及排列组合的应用,求得基本事件与符合条件的基本事件个数是解题的关键.

练习册系列答案
相关题目
如图所示是《函数的应用》的知识结构图,如果要加入“用二分法求方程的近似解”,则应该放在( )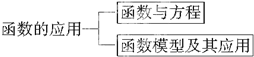

| A、“函数与方程”的上位 |
| B、“函数与方程”的下位 |
| C、“函数模型及其应用”的上位 |
| D、“函数模型及其应用”的下位 |
 如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.
如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.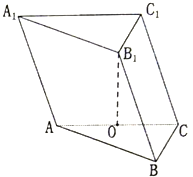 已知三棱柱ABC-A1B1C1的各条棱长均为2,点B1在平面ABC内的射影恰好落在AC边的中点O处.
已知三棱柱ABC-A1B1C1的各条棱长均为2,点B1在平面ABC内的射影恰好落在AC边的中点O处.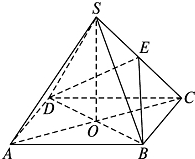 如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,O是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,直线SA和AO所成角的大小是45°.
如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,O是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,直线SA和AO所成角的大小是45°. 在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,∠ACB=90°,AA1=AC=BC=2,D为AB中点.
在三棱柱ABC-A1B1C1中,A1A⊥底面ABC,∠ACB=90°,AA1=AC=BC=2,D为AB中点.