题目内容
已知函数f(x)=log2x与函数y=g(x)的图象关于x=1对称.
(1)求g(x)的解析式,并求其定义域;
(2)若关于x的不等式f(x)+g(x)<log2(x2-2ax+2a+4)(a∈R)恒成立,求实数a的取值范围.
(1)求g(x)的解析式,并求其定义域;
(2)若关于x的不等式f(x)+g(x)<log2(x2-2ax+2a+4)(a∈R)恒成立,求实数a的取值范围.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:(1)由题意可得g(x)=f(2-x),根据解析式求出定义域.
(2)由题意可得x2-(a+1)x+a+2>0在x∈(0,2)上恒成立,令h(x)=x2-(a+1)x+a+2,可得
①
,或②
,或③
.分别求得①、②、③的解集,再取并集,即得所求.
(2)由题意可得x2-(a+1)x+a+2>0在x∈(0,2)上恒成立,令h(x)=x2-(a+1)x+a+2,可得
①
|
|
|
解答:
解:(1)由于函数f(x)=log2x与函数y=g(x)的图象关于x=1对称,
可得g(x)=f(2-x)=log2(2-x),显然定义域为(-∞,2);
(2)∵f(x)+g(x)=log2x+log2(2-x)=log2x(2-x)<log2(x2-2ax+2a+4)恒成立,
∴x(2-x)<x2-2ax+2a+4在x∈(0,2)时恒成立,
即x2-(a+1)x+a+2>0在x∈(0,2)上恒成立.
令h(x)=x2-(a+1)x+a+2,可得
①
,∴
,∴-2≤a≤-1;
或②
,∴
,∴-1<a<3;
或③
∴
,∴3≤a≤4;
综上:-2≤a≤4.
可得g(x)=f(2-x)=log2(2-x),显然定义域为(-∞,2);
(2)∵f(x)+g(x)=log2x+log2(2-x)=log2x(2-x)<log2(x2-2ax+2a+4)恒成立,
∴x(2-x)<x2-2ax+2a+4在x∈(0,2)时恒成立,
即x2-(a+1)x+a+2>0在x∈(0,2)上恒成立.
令h(x)=x2-(a+1)x+a+2,可得
①
|
|
或②
|
|
或③
|
|
综上:-2≤a≤4.
点评:本题主要考查对数函数的图象和性质的综合应用,体现了转化以及分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=4,AD=2,PA=2,PD=
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=4,AD=2,PA=2,PD=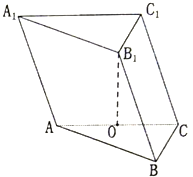 已知三棱柱ABC-A1B1C1的各条棱长均为2,点B1在平面ABC内的射影恰好落在AC边的中点O处.
已知三棱柱ABC-A1B1C1的各条棱长均为2,点B1在平面ABC内的射影恰好落在AC边的中点O处.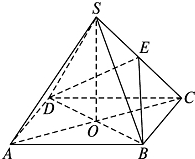 如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,O是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,直线SA和AO所成角的大小是45°.
如图,四棱锥S-ABCD中,底面ABCD是边长为4的正方形,O是AC与BD的交点,SO⊥平面ABCD,E是侧棱SC的中点,直线SA和AO所成角的大小是45°.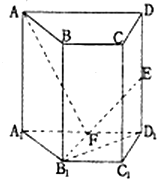 如图,四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,AD⊥DC,AD∥BC,AD=DD1=2,BC=DC=1.点E是侧棱DD1的中点.
如图,四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,AD⊥DC,AD∥BC,AD=DD1=2,BC=DC=1.点E是侧棱DD1的中点.