题目内容
下列命题正确的是（ ）
| A、经过三点，有且只有一个平面 |
| B、平行于同一条直线的两个平面的平行 |
| C、经过平面外一点有且只有一条直线与已知平面平行 |
| D、过一点有且只有一条直线垂直于已知平面 |
考点：命题的真假判断与应用
专题：综合题
分析：A根据平面公理即可判断说法错误；
B举例说明命题错误；
C举例说明命题错误；
D举例并结合证明说明命题正确．
B举例说明命题错误；
C举例说明命题错误；
D举例并结合证明说明命题正确．
解答：
解：对于A，经过不在同一直线上的三点，有且只有一个平面，∴A错误；
对于B，平行于同一条直线的两个平面的不一定平行，
如正方体ABCD-A1B1C1D1中，A1B1∥平面ABCD，A1B1∥平面CDD1C1，但两平面不平行，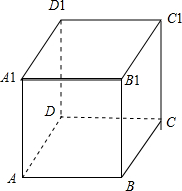
∴B错误；
对于C，如正方体ABCD-A1B1C1D1中，A1B1∥平面ABCD，A1D1∥平面ABCD，
∴经过平面外一点有且只有一条直线与已知平面平行，错误；
对于D，如正方体ABCD-A1B1C1D1中，过A1点只有直线A1A⊥平面ABCD，
反之，如果过点A1还有一条直线A1P⊥平面ABCD，则A1P∥A1A，这与A1P∩A1A矛盾，
假设不成立，即过一点有且只有一条直线垂直于已知平面，正确．
对于B，平行于同一条直线的两个平面的不一定平行，
如正方体ABCD-A1B1C1D1中，A1B1∥平面ABCD，A1B1∥平面CDD1C1，但两平面不平行，
∴B错误；
对于C，如正方体ABCD-A1B1C1D1中，A1B1∥平面ABCD，A1D1∥平面ABCD，
∴经过平面外一点有且只有一条直线与已知平面平行，错误；
对于D，如正方体ABCD-A1B1C1D1中，过A1点只有直线A1A⊥平面ABCD，
反之，如果过点A1还有一条直线A1P⊥平面ABCD，则A1P∥A1A，这与A1P∩A1A矛盾，
假设不成立，即过一点有且只有一条直线垂直于已知平面，正确．
点评：本题通过命题真假的判断，考查了确定平面的条件是什么，空间中的平行与垂直的判断与性质的应用问题，是综合题目．
练习册系列答案
相关题目
已知tanα=4，tan（α-β）=-3，则tanβ=（ ）
A、-
| ||
B、
| ||
C、-
| ||
D、
|
在底面边长为2，高为1的正四梭柱ABCD-A1B1C1D1中，E，F分别为BC，C1D1的中点．则异面直线A1E，CF所成的角为