题目内容
已知b=3，c=1，A=60°，则a= ．
考点：余弦定理
专题：解三角形
分析：根据已知条件，由余弦定理可得 a2=c2+b2-2cb•cosA 的值，从而求得a的值．
解答：
解：在△ABC中，∵已知b=3，c=1，A=60°，
由余弦定理可得 a2=c2+b2-2cb•cosA=1+9-6cos60°=7，
故a=
，
故答案为：
．
由余弦定理可得 a2=c2+b2-2cb•cosA=1+9-6cos60°=7，
故a=
| 7 |
故答案为：
| 7 |
点评：本题主要考查余弦定理的应用，属于基础题．
练习册系列答案
相关题目
sin75°cos255°=（ ）
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
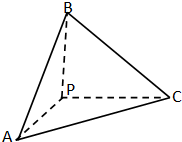三棱锥P-ABC中，三侧棱PA，PB，PC两两互相垂直，且三角形△PAB，△PAC，△PBC的面积依次为1，1，2，则此三棱锥 P-ABC外接球的表面积为（ ）| A、9π | B、12π |
| C、18π | D、36π |
二进制数101 101（2）对应的十进制数是（ ）
| A、45 | B、44 | C、46 | D、47 |
下列函数中，不是奇函数的为（ ）
A、y=ln
| ||
| B、y=-x3 | ||
| C、y=ex+e-x | ||
| D、y=x|x| |
下列命题正确的是（ ）
| A、经过三点，有且只有一个平面 |
| B、平行于同一条直线的两个平面的平行 |
| C、经过平面外一点有且只有一条直线与已知平面平行 |
| D、过一点有且只有一条直线垂直于已知平面 |