题目内容
设不等式组
表示的平面区域为M,若直线l:y=k(x+1)上存在区域M内的点,则k的取值范围是 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,根据直线l:y=k(x+1)过定点(-1,0),结合数形结合即可得到结论.
解答:
解:作出不等式组对应的平面区域如图;
∵直线l:y=k(x+1)过定点A(-1,0),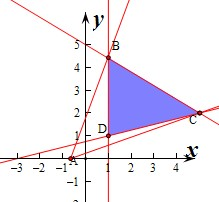
∴要使直线l:y=k(x+1)上存在区域M内的点,
则直线l的斜率k满足kAC≤k≤kAB,
由
,解得
,即B(1,
),
由
,解得
,即C(5,2),
∴kAC=
=
,kAB=
=
,
∴k∈[
,
].
故答案为:[
,
].
∵直线l:y=k(x+1)过定点A(-1,0),

∴要使直线l:y=k(x+1)上存在区域M内的点,
则直线l的斜率k满足kAC≤k≤kAB,
由
|
|
| 22 |
| 5 |
由
|
|
∴kAC=
| 0-2 |
| -1-5 |
| 1 |
| 3 |
| ||
| 1-(-1) |
| 11 |
| 5 |
∴k∈[
| 1 |
| 3 |
| 11 |
| 5 |
故答案为:[
| 1 |
| 3 |
| 11 |
| 5 |
点评:本题主要考查线性规划的应用以及直线斜率公式的计算,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
过双曲线
-
=1(a>0,b>0)的左焦点F(-c,0)(c>0)作圆x2+y2=
的切线,切点为E,延长FE交双曲线右支于点P,若|
|=|
|,则双曲线的离心率( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| 4 |
| OF |
| OP |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在四面体ABCD中,已知AB=x,该四面体的其余五条棱的长度均为2,则下列说法中错误的是( )
A、棱长x的取值范围是:0<x<2
| ||
| B、该四面体一定满足:AB⊥CD | ||
C、当x=2
| ||
| D、当x=2时,该四面体的体积最大 |
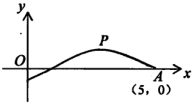 如图,是函数y=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象的一段,O坐标原点,P(3,1)是该段图象的最高点,A(5,0)是该段图象与x轴的一个交点,则此函数的解析式为
如图,是函数y=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象的一段,O坐标原点,P(3,1)是该段图象的最高点,A(5,0)是该段图象与x轴的一个交点,则此函数的解析式为