题目内容
定积分
(|x|-1)dx的值为 .
| ∫ | 1 -1 |
考点:定积分
专题:导数的综合应用
分析:根据分段函数的积分公式进行计算即可.
解答:
解:
(|x|-1)dx=
(-x-1)dx+
(x-1)dx=(-
x2-x)|
+(
x2-x)|
=
-1+
-1=-1,
故答案为:-1.
| ∫ | 1 -1 |
| ∫ | 0 -1 |
| ∫ | 1 0 |
| 1 |
| 2 |
0 -1 |
| 1 |
| 2 |
1 0 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:-1.
点评:本题主要考查积分的计算,根据分段函数的积分公式是解决本题的关键,比较基础.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
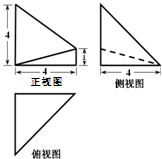 已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V为( )
已知某几何体的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形,则此几何体的体积V为( )A、
| ||
B、
| ||
C、
| ||
| D、40 |
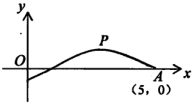 如图,是函数y=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象的一段,O坐标原点,P(3,1)是该段图象的最高点,A(5,0)是该段图象与x轴的一个交点,则此函数的解析式为
如图,是函数y=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象的一段,O坐标原点,P(3,1)是该段图象的最高点,A(5,0)是该段图象与x轴的一个交点,则此函数的解析式为 如图,在△ABC中,已知AB=10,AC=14,B=
如图,在△ABC中,已知AB=10,AC=14,B=