题目内容
设函数f(x)=|x-3|-|x+1|,x∈R.
(Ⅰ)解不等式f(x)<-1;
(Ⅱ)设函数g(x)=|x+a|-4,且g(x)≤f(x)在x∈[-2,2]上恒成立,求实数a的取值范围.
(Ⅰ)解不等式f(x)<-1;
(Ⅱ)设函数g(x)=|x+a|-4,且g(x)≤f(x)在x∈[-2,2]上恒成立,求实数a的取值范围.
考点:绝对值不等式的解法,绝对值不等式
专题:不等式的解法及应用
分析:(Ⅰ根据函数f(x)=
,故由不等式可得 x>3 或
,从而求得不等式的解集.
(Ⅱ)由题意可得当x∈[-2,2]上时,函数g(x)应在函数f(x)的图象的下方,在同一个坐标系中画出函数y=f(x)和y=g(x)的图象,数形结合求得-4≤a≤0,由此求得实数a的取值范围.
|
|
(Ⅱ)由题意可得当x∈[-2,2]上时,函数g(x)应在函数f(x)的图象的下方,在同一个坐标系中画出函数y=f(x)和y=g(x)的图象,数形结合求得-4≤a≤0,由此求得实数a的取值范围.
解答:
 解:(Ⅰ)∵函数f(x)=|x-3|-|x+1|=
解:(Ⅰ)∵函数f(x)=|x-3|-|x+1|=
,
故由不等式f(x)<-1可得 x>3 或
.
解得 x>
.
(Ⅱ)∵函数g(x)=|x+a|-4,且g(x)≤f(x)在
x∈[-2,2]上恒成立,
∴|x+a|-4≤|x-3|-|x+1|在x∈[-2,2]上恒成立,
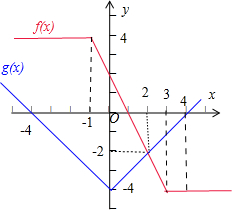
在同一个坐标系中画出函数y=f(x)和y=g(x)的图象,如图所示:
故当x∈[-2,2]时,若0≤-a≤4时,
则函数g(x)在函数f(x)的图象的下方,g(x)≤f(x)在x∈[-2,2]上恒成立,
求得-4≤a≤0,故所求的实数a的取值范围为[-4,0].
 解:(Ⅰ)∵函数f(x)=|x-3|-|x+1|=
解:(Ⅰ)∵函数f(x)=|x-3|-|x+1|=
|
故由不等式f(x)<-1可得 x>3 或
|
解得 x>
| 3 |
| 2 |
(Ⅱ)∵函数g(x)=|x+a|-4,且g(x)≤f(x)在
x∈[-2,2]上恒成立,
∴|x+a|-4≤|x-3|-|x+1|在x∈[-2,2]上恒成立,
在同一个坐标系中画出函数y=f(x)和y=g(x)的图象,如图所示:
故当x∈[-2,2]时,若0≤-a≤4时,
则函数g(x)在函数f(x)的图象的下方,g(x)≤f(x)在x∈[-2,2]上恒成立,
求得-4≤a≤0,故所求的实数a的取值范围为[-4,0].
点评:本题主要考查带由绝对值的函数,绝对值不等式的解法,函数的恒成立问题,体现了转化以及数形结合的数学思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知双曲线标准方程为
-x2=1,则双曲线离心率为( )
| y2 |
| 2 |
A、
| ||||
| B、3 | ||||
C、
| ||||
D、
|
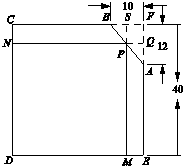 有一块铁皮零件,它的形状是由边长为40cm的正方形CDEF截去一个三角形ABF所得的五边形ABCDE,其中AF长等于12cm,BF长等于10cm,如图所示.现在需要截取矩形铁皮,使得矩形相邻两边在CD,DE上.请问如何截取,可以使得到的矩形面积最大?(图中单位:cm)
有一块铁皮零件,它的形状是由边长为40cm的正方形CDEF截去一个三角形ABF所得的五边形ABCDE,其中AF长等于12cm,BF长等于10cm,如图所示.现在需要截取矩形铁皮,使得矩形相邻两边在CD,DE上.请问如何截取,可以使得到的矩形面积最大?(图中单位:cm)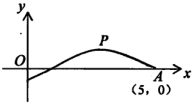 如图,是函数y=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象的一段,O坐标原点,P(3,1)是该段图象的最高点,A(5,0)是该段图象与x轴的一个交点,则此函数的解析式为
如图,是函数y=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象的一段,O坐标原点,P(3,1)是该段图象的最高点,A(5,0)是该段图象与x轴的一个交点,则此函数的解析式为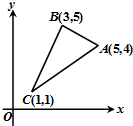 如图,已知可行域为△ABC及其内部,若目标函数z=kx+y当且仅当在点B处取得最大值,则k的取值范围是
如图,已知可行域为△ABC及其内部,若目标函数z=kx+y当且仅当在点B处取得最大值,则k的取值范围是