题目内容
在锐角△ABC中,a、b、c分别为角A、B、C的对边,已知b=2,∠B=
.
(1)若c=2a,求面积S;
(2)求△ABC的周长l及面积S的范围.
| π |
| 3 |
(1)若c=2a,求面积S;
(2)求△ABC的周长l及面积S的范围.
考点:正弦定理,余弦定理
专题:解三角形
分析:(1)利用余弦定理和a与c的关系,求得a和c,最后利用面积公式求得答案.
(2)利用余弦定理建立关于a和c的关系式,利用基本不等式分别求得ac和a+c的范围,进而求得三角形面积和周长的范围.
(2)利用余弦定理建立关于a和c的关系式,利用基本不等式分别求得ac和a+c的范围,进而求得三角形面积和周长的范围.
解答:
解:(1)由余弦定理知cosB=
=
=
,
∴a=
,
∴c=
,
∴S=
acsinB=
×
×
×
=
.
(2)由余弦定理知cosB=
=
=
,整理得(a+c)2=2ac+4,
∵(a+c)2≥4ac,ac≤
∴2ac+4≥4ac,即ac≤2;
≤
,即(a+c)2≤8,a+c≤2
,
∴S=2acsinB=
ac≤2
,l=a+b+c=a+b+2≤2+2
,
∴△ABC的周长的范围(0,2+2
],面积的范围(0,2
].
| a2+c2-b2 |
| 2ac |
| a2+4a2-4 |
| 4a2 |
| 1 |
| 2 |
∴a=
2
| ||
| 3 |
∴c=
4
| ||
| 3 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
4
| ||
| 3 |
| ||
| 2 |
2
| ||
| 3 |
(2)由余弦定理知cosB=
| a2+c2-b2 |
| 2ac |
| (a+c)2-2ac-4 |
| 2ac |
| 1 |
| 2 |
∵(a+c)2≥4ac,ac≤
| (a+c)2 |
| 4 |
∴2ac+4≥4ac,即ac≤2;
| (a+c)2-4 |
| 2 |
| (a+c)2 |
| 4 |
| 2 |
∴S=2acsinB=
| 3 |
| 3 |
| 2 |
∴△ABC的周长的范围(0,2+2
| 2 |
| 3 |
点评:本题主要考查了余弦定理的运用,基本不等式的基础知识.考查了学生分析和推理的能力.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
在等比数列{an}中,a3+a5=6,a4=2
,则a2+a6=( )
| 2 |
A、5
| ||
B、4
| ||
| C、8 | ||
| D、4 |
已知直线l1:2(m+1)x+(m-3)y+7-5m=0和l2:(m-3)x+2y-5=0,若l1⊥l2,则( )
| A、m=-2 | B、m=3 |
| C、m=-1或3 | D、m=3或-2 |
已知两直线l1:3x-4y+7=0和l2:x=-1,点P在抛物线y2=4x上运动,则点P到直线l,和l2的距离之和的最小值是( )
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
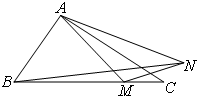 如图已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°(点A,M,N按逆时针方向排列).
如图已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°(点A,M,N按逆时针方向排列).