题目内容
已知函数f(x)=2sinωx(
cosωx-sinωx)+1(ω>0)的最小正周期为3π
(Ⅰ)求不等式f(x)>1的解集;
(Ⅱ)在△ABC中,若f(C)=2,且3sin2A=cosB-sin(B-C),求sinA的值.
| 3 |
(Ⅰ)求不等式f(x)>1的解集;
(Ⅱ)在△ABC中,若f(C)=2,且3sin2A=cosB-sin(B-C),求sinA的值.
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(Ⅰ)首先,借助于二倍角公式和辅助角公式化简函数解析式:f(x)=2sin(2ωx+
),然后,根据周期公式,得到ω=
,最后结合三角函数的图象与性质求解;
(Ⅱ)根据f(C)=2,得到C=
,然后,再借助于三角形中有关的边角关系,得到B=
-A,B-C=-A,代入化简,得到sinA=
.
| π |
| 6 |
| 1 |
| 3 |
(Ⅱ)根据f(C)=2,得到C=
| π |
| 2 |
| π |
| 2 |
| 2 |
| 3 |
解答:
解:(Ⅰ)∵f(x)=2sinωx(
cosωx-sinωx)+1
=2
sinωxcosωx-2sin2ωx+1
=
sin2ωx+cos2ωx
=2sin(2ωx+
)
∴f(x)=2sin(2ωx+
)
∵T=
=3π,
∴ω=
,
∴f(x)=2sin(
x+
),
∵f(x)>1,
∴2sin(
x+
)>1,
∴2sin(
x+
)>
,
∴2kπ+
<
x+
<2kπ+
,k∈Z,
∴3kπ<x<3kπ+π,k∈Z,
∴不等式f(x)>1的解集{x|3kπ<x<3kπ+π,k∈Z };
(Ⅱ)∵f(C)=2,
∴f(C)=2sin(
C+
)=2,
∴sin(
C+
)=1,
∵C∈(0,π),
∴(
C+
)∈(
,
),
∴
C+
=
,
∴C=
,
∴A+B=
,∴B=
-A,B-C=-A,
∵3sin2A=cosB-sin(B-C),
∴3sin2A=cos(
-A)-sin(-A),
∴3sin2A=2sinA,
∵sinA≠0,
∴sinA=
.
∴sinA的值
.
| 3 |
=2
| 3 |
=
| 3 |
=2sin(2ωx+
| π |
| 6 |
∴f(x)=2sin(2ωx+
| π |
| 6 |
∵T=
| 2π |
| 2ω |
∴ω=
| 1 |
| 3 |
∴f(x)=2sin(
| 2 |
| 3 |
| π |
| 6 |
∵f(x)>1,
∴2sin(
| 2 |
| 3 |
| π |
| 6 |
∴2sin(
| 2 |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
∴2kπ+
| π |
| 6 |
| 2 |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
∴3kπ<x<3kπ+π,k∈Z,
∴不等式f(x)>1的解集{x|3kπ<x<3kπ+π,k∈Z };
(Ⅱ)∵f(C)=2,
∴f(C)=2sin(
| 2 |
| 3 |
| π |
| 6 |
∴sin(
| 2 |
| 3 |
| π |
| 6 |
∵C∈(0,π),
∴(
| 2 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴
| 2 |
| 3 |
| π |
| 6 |
| π |
| 2 |
∴C=
| π |
| 2 |
∴A+B=
| π |
| 2 |
| π |
| 2 |
∵3sin2A=cosB-sin(B-C),
∴3sin2A=cos(
| π |
| 2 |
∴3sin2A=2sinA,
∵sinA≠0,
∴sinA=
| 2 |
| 3 |
∴sinA的值
| 2 |
| 3 |
点评:本题重点考查了三角恒等变换公式、二倍角公式、辅助角公式等知识,属于综合题目,中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
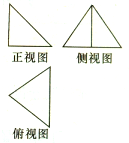 某个几何体的三视图如图所示,其中侧视图是由一个边长为a的正三角形和底边上的高组成,俯视图是正三角形,则该几何体的体积为( )
某个几何体的三视图如图所示,其中侧视图是由一个边长为a的正三角形和底边上的高组成,俯视图是正三角形,则该几何体的体积为( )A、
| ||
B、
| ||
C、
| ||
| D、a3 |
