题目内容
已知圆x2+y2=16与圆（x-4）2+（y+3）2=r2在交点处的切线互相垂直，求实数r的值．
考点：圆的切线方程
专题：直线与圆
分析：根据两个圆切线之间的垂足关系建立条件方程，即可得到结论．
解答：
解：x2+y2=16的圆心O，半径r=4，圆（x-4）2+（y+3）2=r2的圆心是A（4，-3），
设交点之一是B，
因为过B点的切线互相垂直，
所以过B点的两条半径也垂直，
即OB垂直AB
所以三角形OAB是直角三角形，
∠OBA=90°
AO2=（4-0）2+（-3-0）2=25
OB=4，OB2=16
r2=AO2-OB2=9，
即r=3．
设交点之一是B，
因为过B点的切线互相垂直，
所以过B点的两条半径也垂直，
即OB垂直AB
所以三角形OAB是直角三角形，
∠OBA=90°
AO2=（4-0）2+（-3-0）2=25
OB=4，OB2=16
r2=AO2-OB2=9，
即r=3．
点评：本题主要考查圆与圆的位置关系的应用，利用圆的切线之间的关系是解决本题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目
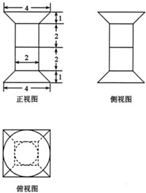一个几何体的三视图如图所示，该几何体从上到下由四个简单几何体组成，其体积分别记为V1，V2，V3，V4，上面两个简单几何体均为旋转体，下面两个简单几何体均为多面体，则V1+V2+V3+V4=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
若某几何体的三视图如图所示（每个正方形的边长均为1），则该几何体的体积等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
