题目内容
在等比数列{an}中,a3+a5=6,a4=2
,则a2+a6=( )
| 2 |
A、5
| ||
B、4
| ||
| C、8 | ||
| D、4 |
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:利用等比数列的首项与公比表示出a3+a5=6,a4=2
,进而联立方程求出公比,再对所求进行化简可得a2+a6=a1(q+q5),即可得到答案.
| 2 |
解答:
解:由题意可得:等比数列{an}中,a3+a5=6,a4=2
,
所以a1q2(1+q2)=6,a1q3=2
,
解得:q=
,a1=1或者q=
,a1=8.
当q=
,a1=1时,a2+a6=a1(q+q5)=5
,
当q=
,a1=8时,a2+a6=a1(q+q5)=5
.
故选:A.
| 2 |
所以a1q2(1+q2)=6,a1q3=2
| 2 |
解得:q=
| 2 |
| ||
| 2 |
当q=
| 2 |
| 2 |
当q=
| ||
| 2 |
| 2 |
故选:A.
点评:解决此类问题的关键是熟练掌握等比数列的通项公式与等比数列的性质,并且结合正确的运算.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知F是抛物线y2=4x的焦点,准线与x轴的交点为M,点N在抛物线上,且|NF|=
|MN|,则∠FMN=( )
| 1 |
| 2 |
| A、30° | B、45° |
| C、60° | D、75° |
函数f(x)=lg(x+1)+lg(x-1)的奇偶性是( )
| A、奇函数 | B、偶函数 |
| C、非奇非偶函数 | D、既奇又偶函数 |
已知函数g(x)=x|a-x|+2x,若存在a∈[-2,3],使得函数y=g(x)-at有三个零点,则实数t的取值范围是( )
A、(
| ||||
B、(2,
| ||||
C、(2,
| ||||
D、(2,
|
复数
(i为虚数单位),Z在复平面内所对应的点在( )
| i-1 |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
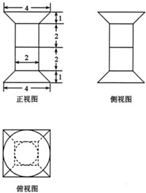 一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V1,V2,V3,V4,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则V1+V2+V3+V4=( )
一个几何体的三视图如图所示,该几何体从上到下由四个简单几何体组成,其体积分别记为V1,V2,V3,V4,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,则V1+V2+V3+V4=( )A、
| ||
B、
| ||
C、
| ||
D、
|
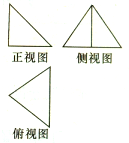 某个几何体的三视图如图所示,其中侧视图是由一个边长为a的正三角形和底边上的高组成,俯视图是正三角形,则该几何体的体积为( )
某个几何体的三视图如图所示,其中侧视图是由一个边长为a的正三角形和底边上的高组成,俯视图是正三角形,则该几何体的体积为( )A、
| ||
B、
| ||
C、
| ||
| D、a3 |