题目内容
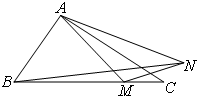如图已知△ABC中，AB=1，AC=2，∠BAC=120°，点M是边BC上的动点，动点N满足∠MAN=30°（点A，M，N按逆时针方向排列）．（1）若
| AN |
| AC |
（2）若
| AM |
| AN |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）由
=2
，得点N在射线AC上，AN=4，再利用余弦定理即可得出；
（2）设∠BAM=x，则∠CAM=120°-x，由于△ABC的面积等于△ABM与△ACM面积的和，可得AM=
，
已知∠MAN=30°，
•
=3，利用数量积可得：AN=4sinx+2
cosx，可得△ABN的面积S=
(4sinx+2
cosx)•sin(x+30°)，再利用倍角公式、两角和差的正弦公式及其单调性即可得出．
| AN |
| AC |
（2）设∠BAM=x，则∠CAM=120°-x，由于△ABC的面积等于△ABM与△ACM面积的和，可得AM=
| ||
2(sinx+
|
已知∠MAN=30°，
| AM |
| AN |
| 3 |
| 1 |
| 2 |
| 3 |
解答：
解：（1）由
=2
，得点N在射线AC上，AN=4，
BN2=1+16-2×1×4×cos120°=21，即BN=
；
（2）设∠BAM=x，则∠CAM=120°-x，
∵△ABC的面积等于△ABM与△ACM面积的和，
∴
•AB•AMsinx+
•AC•AMsin(120°-x)=
•AB•AC•sin120°，
得：AM=
，
又∠MAN=30°，
•
=3，
∴AM•AN•cos30°=3，即AN=4sinx+2
cosx，
∴△ABN的面积S=
(4sinx+2
cosx)•sin(x+30°)=
sin2x+
cos2x+
sinxcosx，
即S=
sin2x-
cos2x+
=
sin(2x-φ)+
．
（其中：sinφ=
，cosφ=
（其中φ为锐角），
∴当2x-φ=90°时，△ABN的面积最大，最大值是
．
| AN |
| AC |
BN2=1+16-2×1×4×cos120°=21，即BN=
| 21 |
（2）设∠BAM=x，则∠CAM=120°-x，
∵△ABC的面积等于△ABM与△ACM面积的和，
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
得：AM=
| ||
2(sinx+
|
又∠MAN=30°，
| AM |
| AN |
∴AM•AN•cos30°=3，即AN=4sinx+2
| 3 |
∴△ABN的面积S=
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 5 |
| 2 |
即S=
| 5 |
| 4 |
| ||
| 4 |
3
| ||
| 4 |
2
| ||
| 4 |
3
| ||
| 4 |
（其中：sinφ=
| ||
2
|
| 5 | ||
2
|
∴当2x-φ=90°时，△ABN的面积最大，最大值是
2
| ||||
| 4 |
点评：本题综合考查了余弦定理、两角和差的正弦余弦公式、倍角公式、三角形的面积公式、三角函数的单调性等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．
练习册系列答案
相关题目
已知函数g（x）=x|a-x|+2x，若存在a∈[-2，3]，使得函数y=g（x）-at有三个零点，则实数t的取值范围是（ ）
A、（
| ||||
B、（2，
| ||||
C、（2，
| ||||
D、（2，
|
设T（x）=|2x-1|，若不等式|a|T（x）≥|a+1|-|2a-1|对任意实数a≠0恒成立，则x的取值范围是（ ）
| A、（-∞，-1]∪[2，+∞） |
| B、（-∞，0]∪[1，+∞） |
| C、[0，1] |
| D、[-1，2] |
若某几何体的三视图如图所示（每个正方形的边长均为1），则该几何体的体积等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|