题目内容
已知两直线l1：3x-4y+7=0和l2：x=-1，点P在抛物线y2=4x上运动，则点P到直线l，和l2的距离之和的最小值是（ ）
| A、2 | ||
B、
| ||
C、
| ||
| D、3 |
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据抛物线 y2=4x，求得抛物线的焦点F和准线，推断出l2为抛物线的准线方程，由抛物线的定义知，P到准线的距离与P到F的距离相等，进而可知抛物线y2=4x上一动点P到直线l1和直线l2的距离之和，即P到F和到直线l1的距离之和的最小值为F到l1的距离．利用点到直线的距离公式求得答案．
解答：
解：∵抛物线 y2=4x
∴焦点F（1，0），准线x=-1，即l2为抛物线的准线方程，
利用抛物线的定义，
P到准线的距离与P到F的距离相等
∴抛物线y2=4x上一动点P到直线l1和直线l2的距离之和即P到F和到直线l1的距离之和．
∴最小值为F到l2的距离．
∴P到直线l，和l2的距离之和的最小值为d=
=
=2，
故选A．
∴焦点F（1，0），准线x=-1，即l2为抛物线的准线方程，
利用抛物线的定义，
P到准线的距离与P到F的距离相等
∴抛物线y2=4x上一动点P到直线l1和直线l2的距离之和即P到F和到直线l1的距离之和．
∴最小值为F到l2的距离．
∴P到直线l，和l2的距离之和的最小值为d=
| |3+7| | ||
|
| 10 |
| 5 |
故选A．
点评：本题主要考查了抛物线的简单性质．解题的过程中特别利用了抛物线的定义，以及数形结合的思想．
练习册系列答案
名校课堂系列答案
相关题目
函数f（x）=lg（x+1）+lg（x-1）的奇偶性是（ ）
| A、奇函数 | B、偶函数 |
| C、非奇非偶函数 | D、既奇又偶函数 |
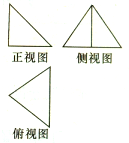某个几何体的三视图如图所示，其中侧视图是由一个边长为a的正三角形和底边上的高组成，俯视图是正三角形，则该几何体的体积为（ ）A、
| ||
B、
| ||
C、
| ||
| D、a3 |
为了解高中生用电脑输入汉字的水平，随机抽取了部分学生进行每分钟输入汉字个数测试，如图是根据抽样测试后的数据绘制的频率分布直方图，其中每分钟输入汉字个数的范围是[50，150]，样本数据分组为[50，70），[70，90），[90，110），[110，130），[130，150]．已知样本中每分钟输入汉字个数小于90的人数是36，则样本中每分钟输入汉字个数不小于70个且小于130个的人数是（ ）若某几何体的三视图如图所示（每个正方形的边长均为1），则该几何体的体积等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|