题目内容
证明：函数f（x）=x2-3是偶函数，且在[0，+∞）上是递增的．
考点：函数奇偶性的判断,函数单调性的性质
专题：函数的性质及应用
分析：根据函数奇偶性和单调性的定义进行判断即可得到结论．
解答：
证明：∵f（x）=x2-3，
∴f（-x）=x2-3=f（x），故函数是偶函数，
设0≤x1＜x2，
则f（x1）-f（x2）=x12-3-（x22-3）=x12-x22=（x1-x2）（x1+x2），
∵0≤x1＜x2，
∴x1-x2＜0，x1+x2＞0，
∴f（x1）-f（x2）=（x1-x2）（x1+x2）＜0，
故f（x1）＜f（x2），
即函数在[0，+∞）上是递增的．
∴f（-x）=x2-3=f（x），故函数是偶函数，
设0≤x1＜x2，
则f（x1）-f（x2）=x12-3-（x22-3）=x12-x22=（x1-x2）（x1+x2），
∵0≤x1＜x2，
∴x1-x2＜0，x1+x2＞0，
∴f（x1）-f（x2）=（x1-x2）（x1+x2）＜0，
故f（x1）＜f（x2），
即函数在[0，+∞）上是递增的．
点评：本题主要考查函数奇偶性和单调性的判断和证明．利用定义法是解决本题的关键．
练习册系列答案
学业测评一课一测系列答案
相关题目
某城市为保护环境，维护水资源，鼓励市民家庭节约用水，作出了如下规定：每月用水不超过4吨，按每吨2元收取消费；每月超过4吨，超过部分加倍收费，某市民家庭某月缴费20元，则该市民家庭这个月实际用水（ ）
| A、7吨 | B、8吨 | C、9吨 | D、10吨 |
函数f（x）=log2|x-1|的图象大致是（ ）
A、 |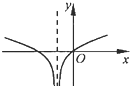
B、 |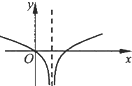
C、 |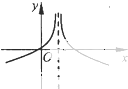
D、 |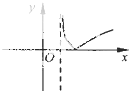
为了得到函数y=
cos2x只需将函数y=
cos(2x+
)的图象（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|