Question

函数f（x）=log₂|x-1|的图象大致是（　　）

• A、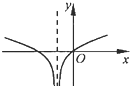
• B、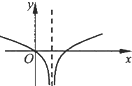
• C、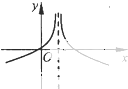
• D、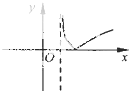

Answer 1

考点：函数的图象

专题：函数的性质及应用

分析：对x的取值进行讨论去掉绝对值符号，转化成对数函数的形式，再结合函数的解析式判断单调性，结合特殊值选出图象．

解答： 解：原函数可化为
y=log₂|x-1|=

log2(x-1)，x＞1 log2(1-x)，x＜1

由复合函数的单调性知x＜1时函数y=log₂（1-x）单调递减，x＞1时函数y=log₂（x-1）单调递增，
且f（

3

2

）=log2(

3

2

-1)=log2

1

2

=-1＜0，
只有图象B符合，
故选：B．

点评：“函数”是贯穿于高中数学的一条主线，函数图象又是表述函数问题的重要工具，因此，巧妙运用函数图象结合函数的解析式，是解题的关键，是基础题．