题目内容
已知命题p:方程
-
=1表示焦点在y轴上的椭圆;命题q:m2-15m<0,若p∧q为假命题,p∨q为真命题,求m的取值范围.
| x2 |
| 2m |
| y2 |
| m-1 |
考点:椭圆的简单性质,复合命题的真假
专题:圆锥曲线的定义、性质与方程
分析:根据题意求出命题p、q为真时m的范围,由p∨q为真,p∧q为假得p真q假,或p假q真,进而求出答案即可.
解答:
解:命题p为真命题时,
将方程
-
=1改写为
+
=1,
只有当1-m>2m>0,即0<m<
时,方程表示的曲线是焦点在y轴上的椭圆,
若命题q为真命题时,
0<m<15,
∵p∧q为假命题,p∨q为真命题,
∴p,q中有一真一假;
当p真q假时,
无解;
当p假q真时,
,解得
≤m<15
综上:m的取值范围为
≤m<15
将方程
| x2 |
| 2m |
| y2 |
| m-1 |
| x2 |
| 2m |
| y2 |
| 1-m |
只有当1-m>2m>0,即0<m<
| 1 |
| 3 |
若命题q为真命题时,
0<m<15,
∵p∧q为假命题,p∨q为真命题,
∴p,q中有一真一假;
当p真q假时,
|
当p假q真时,
|
| 1 |
| 3 |
综上:m的取值范围为
| 1 |
| 3 |
点评:解决问题的关键是熟练掌握命题真假的判定方法,由复合命题的真假判断出简单命题的真假结合有关的基础知识进行判断解题即可.

练习册系列答案
相关题目
已知偶函数y=f(x)在区间[0,+∞)为增函数,则f(-3)和f(π)大小关系是( )
| A、f(-3)>f(π) |
| B、f(-3)<f(π) |
| C、f(-3)=f(π) |
| D、不能确定 |
设f(x-2)=2x,则f(3)的值为( )
| A、64 | B、8 | C、16 | D、32 |
如果命题“p且q”是假命题,“非p”是真命题,那么( )
| A、命题p一定是真命题 |
| B、命题q一定是真命题 |
| C、命题q一定是假命题 |
| D、命题q可以是真命题也可以是假命题 |
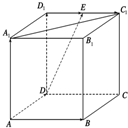 如图所示,在正方体ABCD-A1B1C1D1中,E为D1C1的中点,N为BC的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E为D1C1的中点,N为BC的中点.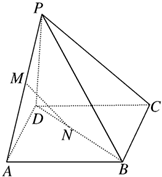 已知正方形ABCD的边长是13,平面ABCD外一点P到正方形各顶点的距离都为13,M、N分别是PA、BD上的点且PM:MA=BN:ND=5:8,如图.
已知正方形ABCD的边长是13,平面ABCD外一点P到正方形各顶点的距离都为13,M、N分别是PA、BD上的点且PM:MA=BN:ND=5:8,如图.