题目内容
18.给出下列五个结论:①回归直线y=bx+a一定过样本中心点($\overline{x}$,$\overline{y}$);
②命题“?x∈R,均有x2-3x-2>0”的否定是:“?x0∈R,使得x02-3x0-2≤0”;
③将函数y=sinx+$\sqrt{3}$cosx的图象向右平移$\frac{π}{6}$后,所得到的图象关于y轴对称;
④?m∈R,使f(x)=(m-1)•x${\;}^{{m}^{2}-4m+3}$是幂函数,且在(0,+∞)上递增;
⑤函数f(x)=$\left\{\begin{array}{l}{x+1,x≤0}\\{{2}^{x}•|lo{g}_{2}x|-1,x>0}\end{array}\right.$恰好有三个零点;
其中正确的结论为( )
| A. | ①②④ | B. | ①②⑤ | C. | ④⑤ | D. | ②③⑤ |
分析 ①根据回归直线的性质进行判断.
②根据含有量词的命题的否定进行判断.
③根据三角函数的图象和性质进行判断.
④根据幂函数的性质进行判断.
⑤根据函数的零点的定义进行判断.
解答 解:①回归直线y=bx+a一定过样本中心点($\overline{x}$,$\overline{y}$);故①正确,
②命题“?x∈R,均有x2-3x-2>0”的否定是:“?x0∈R,使得x02-3x0-2≤0”;故②正确
③函数y=sinx+$\sqrt{3}$cosx=2cos(x-$\frac{π}{6}$),将函数的图象向右平移$\frac{π}{6}$后,得到y=2cos(x-$\frac{π}{6}$-$\frac{π}{6}$)=2cos(x-$\frac{π}{3}$),此时所得到的图象关于y轴不对称;故③错误,
④由m-1=1得m=2,此时f(x)=x0是幂函数,在(0,+∞)上函数不递增;故④错误,
⑤若x≤0则由(x)=0得x+1=0,得x=-1,
若x>0,则由(x)=0得2x|log2x|-1=0,
即|log2x|=($\frac{1}{2}$)x,作出y=|log2x|和y=($\frac{1}{2}$)x的图象,由图象知此时有两个交点,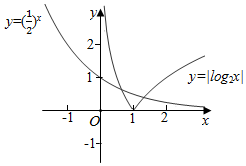
综上函数f(x)=$\left\{\begin{array}{l}{x+1,x≤0}\\{{2}^{x}•|lo{g}_{2}x|-1,x>0}\end{array}\right.$恰好有三个零点;故⑤正确,
故选:B
点评 本题主要考查命题的真假的判断,涉及函数的零点,含有量词的命题的否定,幂函数的定义以及三角函数的图象和性质,综合性较强,考查学生的推理能力.

练习册系列答案
相关题目
8.已知椭圆具有如下性质:若椭圆的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),则椭圆在其上一点A(x0,y0)处的切线方程为$\frac{{{x_0}x}}{a^2}+\frac{{{y_0}y}}{b^2}$=1,试运用该性质解决以下问题:椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),其焦距为2,且过点$(1,\frac{{\sqrt{2}}}{2})$.点B为C1在第一象限中的任意一点,过B作C1的切线l,l分别与x轴和y轴的正半轴交于C,D两点,则△OCD面积的最小值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
3.已知θ为第一象限的角,sinθ-2cosθ=-$\frac{2}{5}$,则sinθ+cosθ等于( )
| A. | $\frac{9}{5}$ | B. | $\frac{8}{5}$ | C. | $\frac{7}{5}$ | D. | $\frac{6}{5}$ |